最长公共子序列

步骤 1：刻画最长公共子序列

暴力求解的穷举法绝对是一个坏主意，因为其运行时间为指数阶。所以我们要来寻找 LCS 的最优子结构。最优子结构如下：

令 X = 和 Y = 为两个序列，Z = 为 X 和 Y 的任意 LCS。 1. 如果 xm = yn，则 zk=xm=yn 且 Z(k-1)是 X(m-1)和 Y(n-1)的一个 LCS。 2. 如果 xm != yn，那么 zk != xm 意味着 Z 是 X(m-1)和 Y 的一个 LCS。 3. 如果 xm != yn，那么 zk != yn 意味着 Z 是 X 和 Y(n-1)的一个 LCS。

第一条很好理解，如果 xm = yn，则只是把 LCS 的长度加 1 即可。第二条和第三条就不是那么直观了，大概意思就是如果 xm != yn，则 Z 是 X(m-1)和 Y 或者是 X 和 Y(n-1)的一个 LCS。LCS 的长度实质上没有改变，只是跳过了一个 xm 或 yn 而已，因为在这一步中 xm 和 yn 不等，所以 LCS 没变。

步骤 2：一个递归解

如步骤 1 所述，如果 xm = yn，我们应该求解 X(m-1)和 Y(n-1)的一个 LCS，然后将 xm = yn 添加到这个 LCS 的末尾，就得到了 X 和 Y 的 LCS。如果 xm != yn，我必须求解两个子问题，X(m-1)和 Y 的 LCS 与 X 和 Y(n-1)的 LCS，然后将其中较长的作为 X 和 Y 的 LCS。因为这些情况覆盖了所有的可能，所以必然有一个最优解出现在 X 和 Y 的 LCS 中。另外 LCS 的重叠子问题性质也很明显，在求解 X 和 Y 的 LCS 时，我们会需要 X 和 Y(n-1)的 LCS 及 X(m-1)和 Y 的 LCS，也需要求解 X(m-1)和 Y(n-1)的子问题。

定义 c[i, j]表示 X(i)和 Y(j)的 LCS 长度，由上述的讨论我们可以得到递归公式：

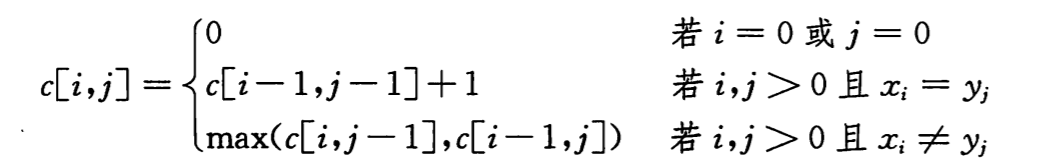
最长公共子序列1.png

步骤 3：计算 LCS 的长度

采用自底向上的方法，用表 c 存储 LCS 长度，用表 b[i, j]存储对应计算 c[i, j]时所选择的子问题最优解，然后按行主次序计算表项。具体计算方法见下文的完整 C 语言代码。

下图显示了输入序列 X = 和 Y = 生成的表 c 和表 b（两张表放在了同一张图中），运行时间为Θ(mn)。注意图中显示了两个不同的 LCS，长度均为 4。

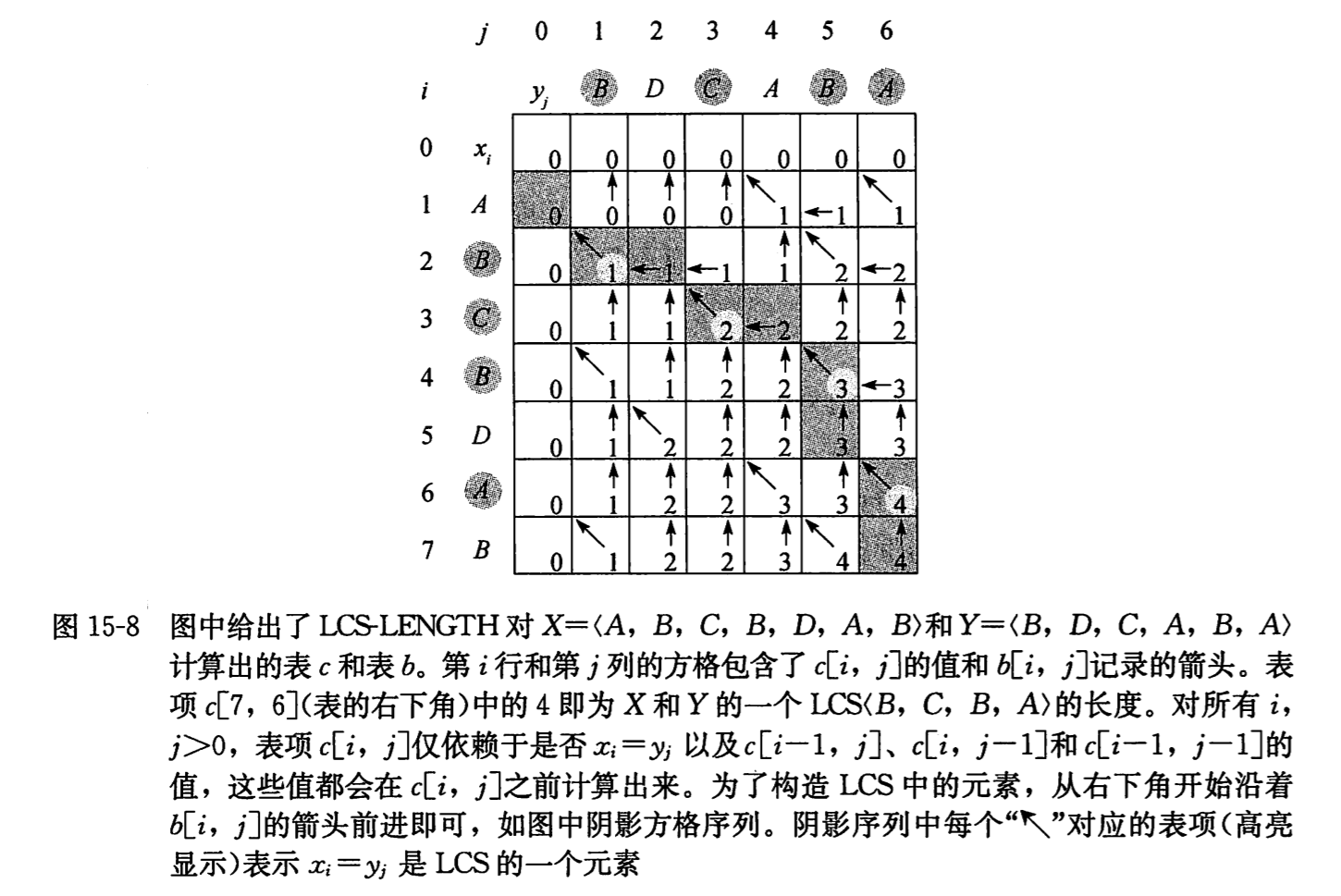
最长公共子序列2.png

步骤 4：构造 LCS

利用表 b，将其递归展开，就可以得到一个 LCS。简单地从 b[m ,n]开始，然后按箭头的方向追踪下去即可，当遇到一个”↖”时，就意味着 xi = yj 是 LCS 的一个元素。同样，具体实现见下本的 C 语言代码。

C 语言实现

动态规划法解 LCS 问题的 C 语言实现如下，其中包含了两个例子，一个是上文中的 ABCD 的例子，又一个是算法导论中求 DNS 串相似度的例子：

    #include <stdlib.h>
    #include <stdio.h>

    /* DNA串 例1 */
    #define A   1
    #define C   2
    #define G   3
    #define T   4

    /* 简单的ABCD 例2 */
    /* #define A   1 */
    /* #define B   2 */
    /* #define C   3 */
    /* #define D   4 */

    #define UPRIGTH     5
    #define UP          6
    #define LEFT        7

    /* 例1 */
    #define XLEN       29
    #define YLEN       28

    /* 例2 */
    /* #define XLEN       7 */
    /* #define YLEN       6 */

    void
    lcs_length(int *x, int *y, int c[XLEN + 1][YLEN + 1], int b[XLEN + 1][YLEN + 1])
    {
        int     i, j;

        for (i = 0; i <= XLEN; i++)
            c[i][0] = 0;
        for (j = 0; j <= XLEN; j++)
            c[0][j] = 0;

        for (i = 1; i <= XLEN; i++)
            for (j = 1; j <= YLEN; j++) {
                if (x[i] == y[j]) {
                    c[i][j] = c[i - 1][j - 1] + 1;
                    b[i][j] = UPRIGTH;
                } else if (c[i -1][j] >= c[i][j - 1]) {
                    c[i][j] = c[i - 1][j];
                    b[i][j] = UP;
                } else {
                    c[i][j] = c[i][j - 1];
                    b[i][j] = LEFT;
                }
            }
    }

    void
    print_elem(int x)
    {
        switch(x) {
            case A:
                printf("A");
                break;
            /* case B: */
                /* printf("B"); */
                /* break; */
            case C:
                printf("C");
                break;
            /* case D: */
                /* printf("D"); */
                /* break; */
            case G:
                printf("G");
                break;
            case T:
                printf("T");
                break;
            default:
                printf("0");
        }
    }

    void
    print_arrow(int x)
    {
        switch(x) {
            case UPRIGTH:
                printf("↖ ");
                break;
            case UP:
                printf("↑ ");
                break;
            case LEFT:
                printf("← ");
                break;
            default:
                printf("0 ");
        }
    }

    int
    print_lcs(int b[XLEN + 1][YLEN + 1], int *x, int i, int j)
    {
        if (i == 0 || j == 0)
            return(0);
        if (b[i][j] == UPRIGTH) {
            print_lcs(b, x, i -1, j - 1);
            print_elem(x[i]);
        } else if (b[i][j] == UP) {
            print_lcs(b, x, i - 1, j);
        } else {
            print_lcs(b, x, i, j - 1);
        }
    }

    int
    main(void)
    {
        int     n, m;
        int     i, j;
        /* 例1 */
        int     x[XLEN + 1] = {0,A,C,C,G,G,T,C,G,A,G,T,G,C,G,C,G,G,A,A,G,C,C,G,G,C,C,G,A,A};
        int     y[YLEN + 1] = {0,G,T,C,G,T,T,C,G,G,A,A,T,G,C,C,G,T,T,G,C,T,C,T,G,T,A,A,A};
        /* 例2 */
        /* int     x[XLEN + 1] = {0, A, B, C, B, D, A, B}; */
        /* int     y[YLEN + 1] = {0, B, D, C, A, B, A}; */

        int     c[XLEN + 1][YLEN + 1] = {0};
        int     b[XLEN + 1][YLEN + 1] = {0};

        lcs_length(x, y, c, b);

        printf("table b:\n");
        for (i = 0; i <= XLEN; i++) {
            for (j = 0; j <= YLEN; j++) {
                print_arrow(b[i][j]);
            }
            printf("\n");
        }
        printf("\n");

        printf("table c:\n");
        for (i = 0; i <= XLEN; i++) {
            for (j = 0; j <= YLEN; j++)
                printf("%2d ", c[i][j]);
            printf("\n");
        }
        printf("\n");

        printf("sequence X: ");
        for (i = 1; i <= XLEN; i++)
            print_elem(x[i]);
        printf("\n");
        printf("sequence Y: ");
        for (i = 1; i <= YLEN; i++)
            print_elem(y[i]);
        printf("\n");

        printf("LCS: ");
        print_lcs(b, x, XLEN, YLEN);

        return 0;
    }