动态规划:钢铁切割
动态规划与分治法相似,都是通过组合子问题的解来求解原问题。分治方法将问题划分为互不相交的子问题,递归地求解子问题,即不同的子问题具有公共的子子问题。在这种情况下,分治算法会反复地求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都重新计算,避免了不必要的计算工作。
动态规划方法通常用来求解*最优化问题*。这类问题有很多个可行解,每个解都有一个值,我们需要寻找具有最优值的解。
通常按如下 4 个步骤来设计一个动态规划算法: 1. 刻画一个最优解的结构特征。 2. 递归地定义最优解的值。 3. 计算最优解的值,通常采用自底向上的方法。 4. 利用计算出的信息构造一个最优解
步骤 1~3 是动态规划求解问题的基础,如果仅仅需要一个最优解的值,而非解本身,可以忽略步骤 4。
钢铁切割
先通过一个例子来直观的学习一下动态规划。
*切割钢铁问题*是这样的,给定一段长度为 n 的钢铁和一个价格表 p,求切割钢铁方案,使得收益 r 最大。
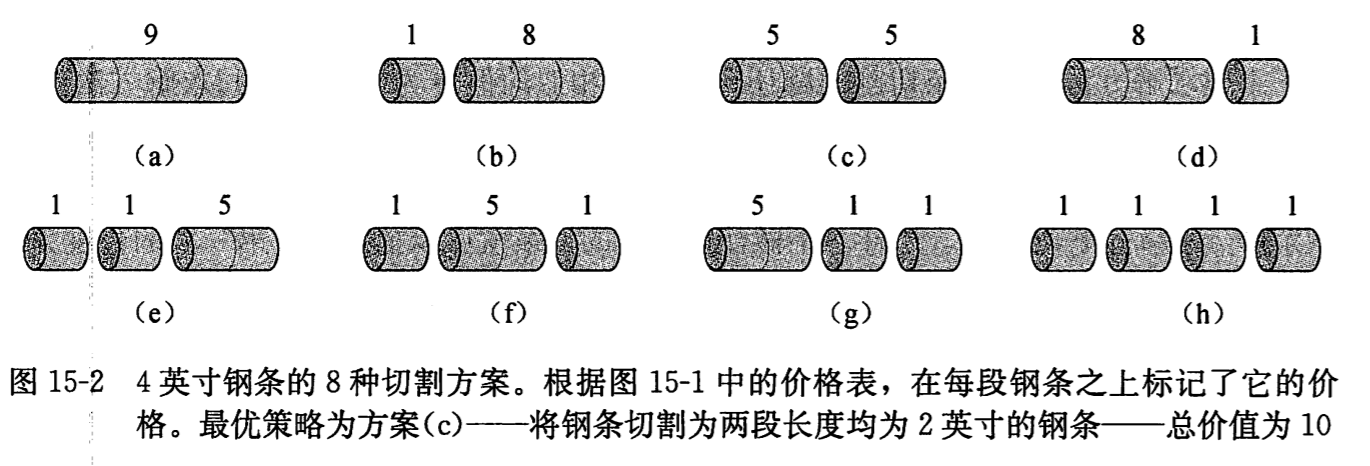
长度为 n 的钢铁有 2\^(n-1)种不同的切割方案。一般而言,对于最大收益 rn,我们可以如下公式来描述:
rn = max(pn, r1+rn-1, r2+rn-2, …, rn-1+r1)
pn 对应不切割,直接出售长度为 n 的钢条。另外你 n-1 个参数对应 n-1 个方案:对于每个 i,首先将钢条切割为长度 i 和 n-i 两段,接着球这两段的最优切割收益 ri 和 rn-1。我们不知道哪种方案会获得最优收益,所以必须考察所有可能的 i,选出其中最大值。
注意到,为了求解规模为 n 的原问题,我们先求解形式完全一样,但规模更小的子问题。即首次切割之后,将切割后的两段钢条看作两个独立的钢条切割问题。通过组合两个相关子问题的最优解,并在所有可能的两端切割方案中选取组合收益最大的,构成原问题的最优解。我们称钢条切割问题满足*最优子结构*性质:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
除了上述求解方法外,还存在一种更为简单的递归求解方法:将钢条从左边切割下长度为 i 的一段,然后只对右边剩下的长度为 n-i 的一段继续进行切割(递归求解)。即将长度为 n 的钢条分解为左边开始一段,以及剩余部分继续分解的结果。于是我们可以得到上面公式的简化版本:
rn = max(pi + rn-i)
自顶向下的递归实现
有了上面的公式,我们就可以使用 C 语言递归求解钢条切割问题了:
#include <stdlib.h> #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int cut_rod(int *p, int n) { int i, q; if (n == 1) return(0); q = -65535; for (i = 1; i < n; i++) { q = MAX(q, p[i] + cut_rod(p, n - i)); } return(q); } int main(int argc, const char *argv[]) { int p[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30}; int max; max = cut_rod(p, 11); printf("%d\n", max); return 0; }
在价格数组最前加个 0,是为了够能使函数 cut\_rod 正确运行,令 i 从 1 开始,不会造成无限循环的问题。在实际求解问题的过程中,一旦输入的规模稍微变大,运行时间就成倍的增长。n每增大 1,运行时间就会增加一倍。实际上,cut\_rod 的运行时间是 n 的指数函数,会爆炸性的增长。 当 n=10 时,运行时间都不会觉察到,当 n=20 时,大概会运行 20 秒,当 n=30 时,运行了 1 个小时都还没有结果……
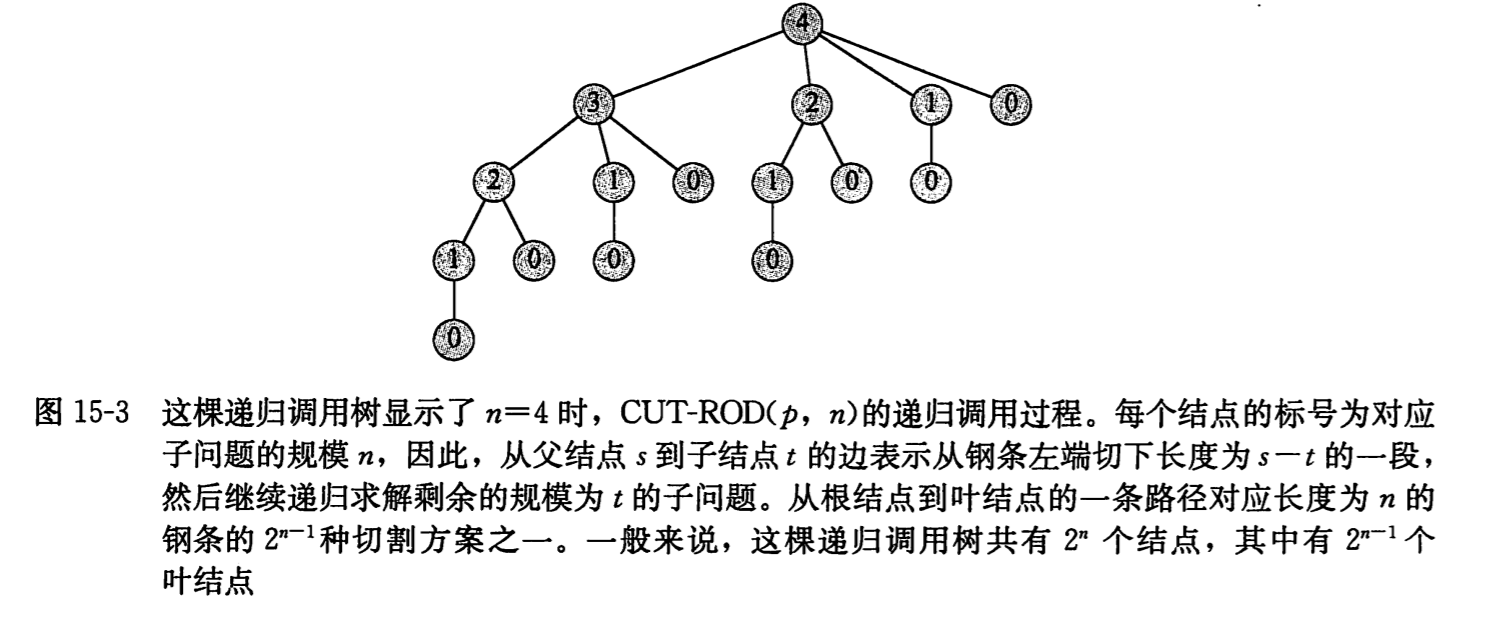
递归算法效率这么查的原因在于它反复地用相同的参数对自身进行调用。下图显示了 n 为 4 时的调用过程。
动态规划方法求解问题
与一开始说的一样,动态规划方法仔细安排求解的顺序,对每个子问题只求解一次,并将结果保存下来。如果之后再次遇到此子问题,只需查找保存的结构,而不必重新计算。所以,动态规划是付出额外的内存空间来节省计算时间,典型的时空权衡的例子,而且时间上的节省可能是非常巨大的。
动态规划有两种等价的实现方法:
第一种方法称为 带备忘的自顶向下法 。此方法仍然是按递归形式编写,但过程会保存每个子问题的解(保存在数组或散列表中)。当需要一个子问题的解时,会首先检查是否已经保存了这个解。
第二种方法成为 自底向上法 。这种方案一般需要恰当的定义子问题“规模”的概念,使得任何子问题的求解都只依赖于“更小的”子问题求解。因此可以将子问题排序,按由大到小的顺序进行求解。当求解某个子问题时,它所依赖的那些更小的子问题都已求解完毕,结果已经保存。
这两种方法的渐进运行时间相同,仅有的差异在某些特殊情况下,自顶向下方法并未真正的考察所有可能的子问题。另外,由于没有频繁的递归函数调用,自底向上的方法时间复杂度通常有更小的系数。
以下分别是自顶向下和自底向上解钢条切割问题的 C 语言实现:
#include <stdlib.h> #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int memized_cut_rod_aux(int *p, int n, int *r) { /* *自顶向下 */ int i, q; if (r[n - 1] >= 0) return(r[n - 1]); if (n == 1) q = 0; else { q = -65535; for (i = 1; i < n; i++) { q = MAX(q, p[i] + memized_cut_rod_aux(p, n - i, r)); } } r[n - 1] = q; return(q); //返回最优解 } int memized_cut_rod(int *p, int n) { int i, *r, max; r = (int *)malloc(n * sizeof(int)); for (i = 0; i < n; i++) { r[i] = -65535; } max = memized_cut_rod_aux(p, n, r); free(r); return(max); } int bottom_up_cut_rod(int *p, int n) { /* *自底向上 */ int i, j, q; int r[n]; r[0] = 0; //长度为0的钢条没有收益 for (j = 1; j < n; j++) { q = -65535; for (i = 1; i <= j; i++) q = MAX(q, p[i] + r[j - i]); r[j] = q; //保存子问题的最优解 } return(r[n - 1]); //返回最优解 } int main(int argc, const char *argv[]) { int p[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30}; int max; /* max = memized_cut_rod(p, 11); */ max = bottom_up_cut_rod(p, 11); printf("%d\n", max); return 0; }
自顶向下法中,主过程 memized\_cut\_rod 将辅助数组 r 初始化为一个负值,表示尚未保存任何子问题的解。然后调用辅助过成 memized\_cut\_rod\_aux,它与递归法类似,只是保存子问题的解,并在一开始 i 检查所需的解是否已知(r[n]>= 0)。
自底向上法,bottom\_up\_cut\_rod 采取子问题的自然顺序依次对其进行求解。求解时采用的公式相同,只是直接访问数组元素 r[j - i]来获得子问题规模为 j – i 的解,而不进行递归调用。
两种方法的渐进运行时间都是Θ(n\^2)。
子问题图
当思考一个动态规划问题时,我们应该弄清所涉及的子问题及子问题之间的依赖关系。
问题的 子问题图 准备地表达了这些信息。下图显示了 n=4 时钢条切割问题的子问题图。它是一个有向图,每个顶点唯一地对应一个子问题。若求子问题 x 的最优解时需要直接用到子问题 y 的最优解,那么在子问题图中就会有一条从 x 到 y 的有向边。我们可以把子问题图看作自顶向下递归树的简化版,因为树中所有相同的子问题结点都合并为了图中的单一顶点。
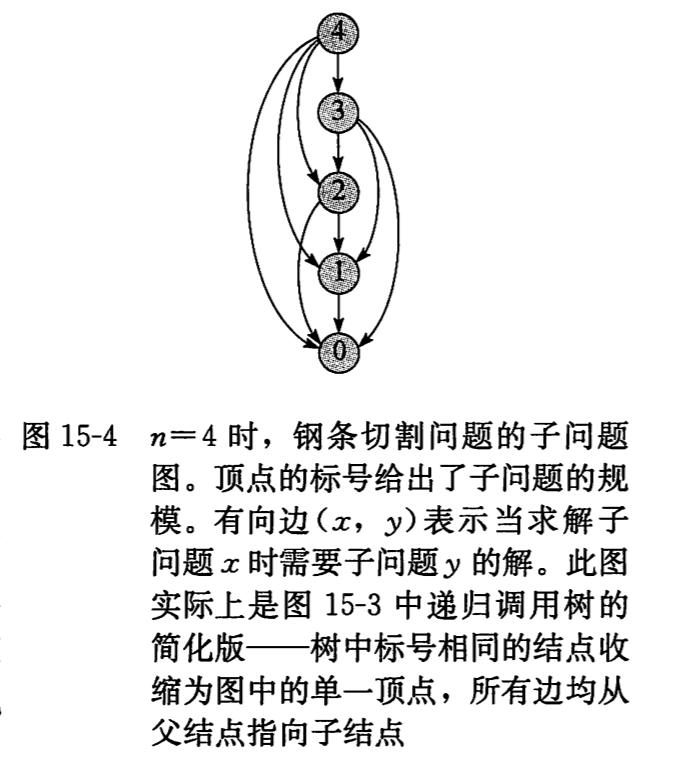
子问题图的规模还可以帮助我们确定动态规划算法的运行时间。由于每个子问题只求解一次,因此算法的运行时间等于每个子问题求解时间之和。通常,一个子问题的求解时间与子问题图中对应顶点的度成正比。
重构解
前面给出的算法的 C 语言实现只给出了问题的最优解的收益值,但是并没有返回最优解本身。我们可以扩展动态规划算法,使之对每个子问题不仅保存收益值,还保存对应的切割方案。利用这些信息,就可以输出最优解。下面的 C 语言代码将最优解对应的第一段钢条切割长度保存在数组 s 中,然后重构并输出最优解:
void extended_bottom_up_cut_rod(int *p, int n, int *r, int *s) { int i, j ,q; r[0] = 0; for (j = 1; j < n; j++) { q = -65535; for (i = 1; i <= j; i++) { if (q < p[i] + r[j - i]) { q = p[i] + r[j - i]; s[j] = i; } } r[j] = q; } } void print_cut_rod_solution(int *p, int n) { int r[n], s[n]; extended_bottom_up_cut_rod(p, n, r, s); while (n - 1 > 0) { printf("%d ", s[n - 1]); n = n - s[n - 1]; } printf("\n"); }
对于前面给出的钢条切割实例,extended_bottom_up_cut_rod 会返回下面的数组: