堆排序和优先队列

堆排序

堆排序的时间复杂度是 O(nlgn)，同时还具有空间原址性，所以堆排序集合了插入排序和归并排序两种算法优点的一种排序算法。

（二叉）堆 是一个数组，它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左向右填充。

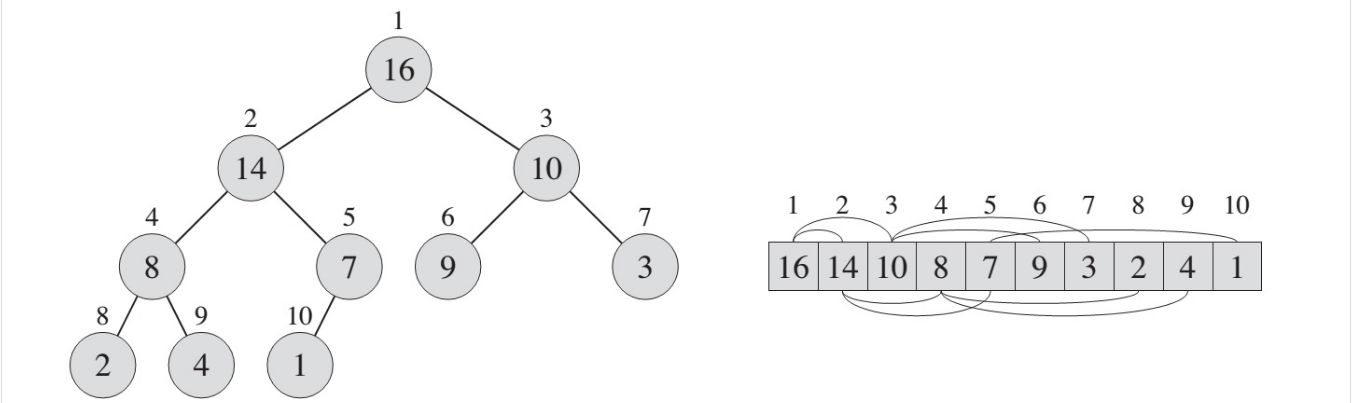
数组上方和下方的连线显示的是父子关系：父节点总是在其孩子结点的左边。

最大堆指的是除了根节点以外的所有结点的值至多与其父节点一样大。而最小堆则正好相反，最小堆中的最小元素存放在根节点中。在堆排序算法中，使用的是最大堆，最小堆通常用于构造优先队列。 C 语言堆排序代码：

    #include <stdlib.h>

    //#define PARENT(i)       ((i) / 2)       //返回其父节点
    #define LEFT(i)         (2 * (i) + 1)     //返回其左孩子节点
    #define RIGHT(i)        (2 * (i) + 2)     //返回其右孩子节点
    #define exchange(a, b)  {(a) = (a) + (b); (b) = (a) - (b); (a) = (a) - (b);}

    int heapsize, length;

    void
    max_heapify(int *A, int i)
    {
        /*
         * 从A[i], A[LEFT(i)], A[RIGHT(i)]中选出最大的，
         * 并将其下标存储在largest中。如果A[i]是最大的
         * 那么以i为根结点的子树已经是最大堆，程序结束。
         * 否则最大元素是i的某个孩子节点，则交换A[i]和
         * A[largest]的值，然后递归向下因为刚刚的改动
         * 可能会违反最大堆性质。
         */
        int     l, r, largest;

        l = LEFT(i);
        r = RIGHT(i);

        if (l < heapsize && A[l] > A[i]) {
            largest = l;
        } else {
            largest = i;
        }

        if (r < heapsize && A[r] > A[largest]) {
            largest = r;
        }

        if (largest != i) {
            exchange(A[i], A[largest]);
            max_heapify(A, largest);
        }
    }

    void
    build_maxheap(int *A)
    {
        /*
         * 子数组A(n / 2 + 1..n)中的元素都是树的叶节点，
         * 该过程对树中的其他节点都调用一次max_heapify。
         */
        int     i;

        for (i =  (length - 1) / 2; i >= 0; i--) {
            max_heapify(A, i);
        }
    }

    void
    heapsort(int *A)
    {
        /*
         * 数组中的最大元素总在根节点A[0]中，把它与A[i]交换，
         * 我们可以让该元素放到正确的位置。然后通过heapsize-1
         * 来从堆中去掉该节点。在交换完毕后，剩余的节点可能会
         * 违反最大堆性质，所以调用max_heapify维护最大堆
         */
        int     i;

        build_maxheap(A);
        for (i = length - 1; i >= 1; i--) {
            exchange(A[0], A[i]);
            heapsize = heapsize - 1;
            max_heapify(A, 0);
        }
    }

    int
    main(void)
    {
        int i;
        int A[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};

        heapsize  = sizeof(A) / sizeof(int);
        length = heapsize;

        heapsort(A);

        for (i = 0; i < 10; i++)
            printf("%d ", A[i]);
        printf("\n");

        return(0);
    }

虽然堆排序是一个优秀的算法，但是在实际应用中，快速排序的性能一般会优于堆排序。

优先队列

优先队列 （priority queue）是一种用来维护由一组元素构成的集合的数据结构，其中的每一个元素都有一个相关的 关键值 （ key）。一个 最大优先队列 支持以下操作：

    #define MIN             -65535

    int
    heap_max(int *A)
    {
        /*
         * 返回A中具有最大关键字的元素
         */
        return A[0];
    }

    int
    heap_extract_max(int *A)
    {
        /*
         * 去掉并返回A中具有最大关键字的元素
         */
        int     max;

        if (heapsize < 1) {
            printf("heap underflow\n");
            return(-1);
        }

        max = A[0];
        A[0] = A[heapsize];
        heapsize--;
        max_heapify(A, 0);
        return(max);
    }

    void
    heap_increase_key(int *A, int i, int key)
    {
        /*
         * 将元素i的关键字值增加到key，key不小于i的源关键字值
         */
        int     i;

        if (key < A[i]) {
            printf("new key is smaller than current key\n");
        }
        A[i] = key;
        while (i > 0 && A[PARENT(i)] < A[i]) {
            exchange(A[i], A[PARENT(i)]);
            i = PARENT(i);
        }
    }

    void
    max_heap_insert(int *A, int key)
    {
        /*
         * 把元素x插入集合A中
         */
        heapsize++;
        A[heapsize] = MIN;
        heap_increase_key(A, heapsize, key);
    }

堆排序和优先队列

目录

堆排序

优先队列