摊还分析:动态表
对某些应用程序,我们无法预先知道会将多少个元素存储在表中。我们为一个表分配一定的内存空间,随后可能会发现不够用。于是为其重新分配更大的空间,并将所有对象从原表中复制到新的空间中。类似地,如果从表中删除了很多元素,可能为其重新分配一个更小的内存空间是值得的。本文我们使用摊还分析来证明,虽然表在扩张和收缩时有较高的实际代价,但它们的摊还代价都是О(1),且表中的空间空间与总空间的比例永远不会超过一个常量分数。为了方便分析,我们将一个非空表 T 的*装载因子*α(T)定义为表中存储的数据项的数量除以表的规模,一个规模为 0 的空表α(T) = 1。
表扩张
一个常用的分配新表的启发式策略是:当旧表被填满时,我们为新表分配 2 倍旧表的槽。如果只允许插入操作,那么装载因子总是保持在 1/2 以上,因此,浪费的空间永远不会超过总空间的一半。
令 T.table 保存指向表的存储空间的指针,T.num 保存表中的数据数量,T.size 保存表的规模,其伪代码如下:
if T.size == 0
allocate T.table with 1 slot
T.size = 1
if T.num == T.size
allocate new-table with 2*T.size slot
insert all items in T.table into new-table
free T.table
T.table = new-table
T.size = 2*T.size
insert x into T.table
T.num = T.num + 1
我们将每次插入一个元素的代价设定为 1,然后用插入元素的次数来描述 TABLE-INSERT 的运行时间。设第 i 个操作的代价为 ci,一个操作的最坏情况发生在需要表扩张时,如果执行 n 个操作,一个操作的最坏情况时间为Ο(n),从而可以的到 n 个操作的总运行时间上界Ο(n\^2)。
当然这不是一个紧确界,因为实际上仅当 i-1 恰好为 2 的幂时,第 i 个操作才会引起一次扩张,所以第 i 个操作的代价为
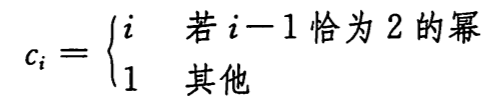
因此 n 个 TABLE-INSERT 操作的总代价为
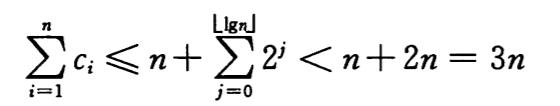
由于 n 个 TABLE-INSERT 操作的总代价以 3n 为上界,所以单一操作的摊还代价仅为 3。
如果使用核算法,则插入一个元素的 3 个代价其实分别为:插入到当前表中的代价,当表扩张时移动它的代价,当表扩张时移动另一个已经移动过一次的数据项。前一个是插入元素的实际代价,我们将后两个代价存为信用,这样在表需要扩张的时候,表中的每一个数据项都储存了 1 个代价,可以用来支付扩张时插入到新表的代价。
另外我们还可以使用势能法来分析。定义一个势函数Φ,在扩张操作之后其值为 0,而表满时其值为表的规模,这样就可以用势能来支付下次扩张的代价。则势函数为
Φ(T) = 2*T.num – T.size
为了分析第 i 个 TABLE-INSERT 操作的摊还代价,我们另 numi 表示第 i 个操作后表中数据数量,sizei 表示第 i 个操作后的总规模,Φi 表示第 i 个操作后的势。则如果第 i 个操作没有触发扩张,size(i) = size(i-1),则摊还代价为
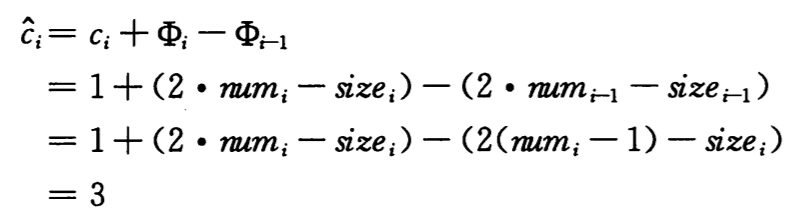
如果第 i 个操作触发了扩张,则 size(i) = 2/size(i-1)及 size(i-1) = num(i-1) = num(i)-1,也就是 size(i) = 2/(num(i) – 1)。所以其摊还代价为
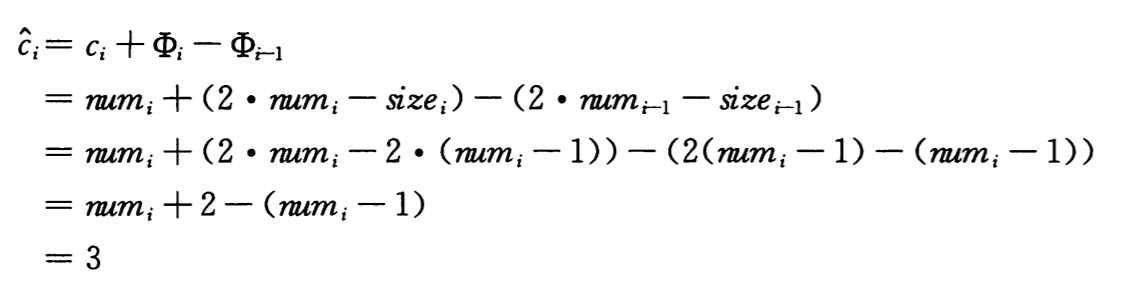
下图画出了 num(i)、size(i)和Φ(i)随 i 变化的情况。注意势是如何累积来支付表扩张代价的,另外在每次扩张之后,势变为 0,但会立即变为 2-–—引起扩张的那个数据被插入表中。
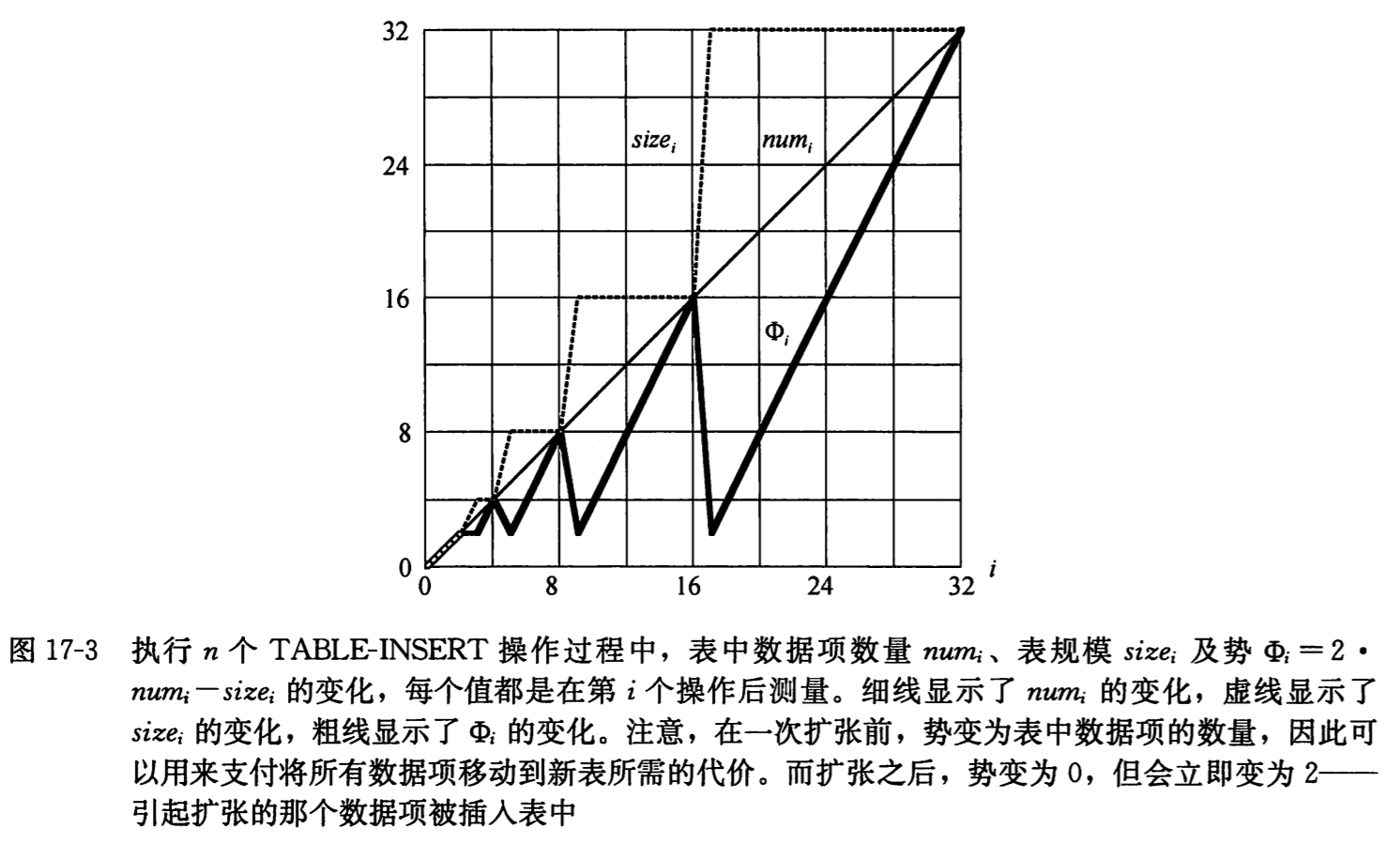
表扩张和收缩
表收缩和表扩张是类似的操作所以省略的收缩的叙述及伪代码。理想情况下,我们希望表收缩的时候保持两个性质:
- 动态表的装载因子有一个正的常数的下界
- 一个表操作的摊还代价有一个常数上界
我们假定用元素的插入、删除次数来衡量动态表操作的代价。
你可能认为当插入一个数据到满表时应该将其扩张,当删除一个数据导致装载因子小于 1/2 时就应该将表规模减半。此策略可以保证表的装载因子永远不会低于 1/2,但遗憾的是,这回导致操作的瘫痪代价过大。考虑如下场景,对一个表 T 执行 n 个操作,n恰好是 2 的幂。其中前 n/2 个操作都是插入,由之前的分析可知其总代价为Θ(n)。插入序列结束时,T.num = T.size = n/2。接下来 n/2 个操作是这样的:
插入、删除、删除、插入、插入、删除、删除、插入、插入、……
第一个插入导致表扩张至 n,接下来两个删除导致表收缩为 n/2,再接下来两个插入又导致表扩张为 n,依此类推。收缩和扩张的次数将为Θ(n),每次扩张和收缩的代价为Θ(n)。因此,n个操作的总代价为Θ(n\^2),每个操作的摊还代价为Θ(n)。
此策略的缺点是明显的:在表扩张之后,我们无法删除足够多的数据项来为收缩操作支付费用;类似地,在表收缩之后,我们无法插入足够多的表项来支付扩张操作。
我们可以改进此策略,当向一个满表插入一个新数据项时,我们仍然将表规模加倍,但是只有当装载因子小于 1/4 而不是 1/2 时,才将表规模减半。
可能我们直觉上认为装载因子为 1/2 比较理想,而表的势此时为 0。随着装载因此偏离 1/2,势应该增长,使得当扩张或收缩表时,表已经储存了足够的势来支付复制所有数据到新表的代价。因此,我们需要一个势函数,当装载因子增长为 1 或下降为 1/4 时,势函数值增长为 T.num。而表扩张或收缩之后,装载因子重新变为 1/2,而表的势降回 0。因此可以得到势函数如下:
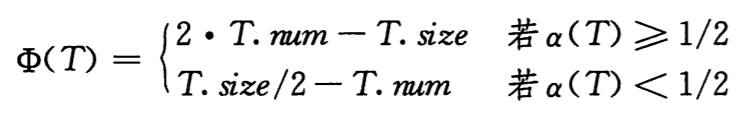
空表时势为 0,且势永远不可能为负,所以势函数定义的操作序列的总摊还代价是总实际代价的上界。
下图画出了 num(i)、size(i)和Φ(i)随 i 变化的情况。
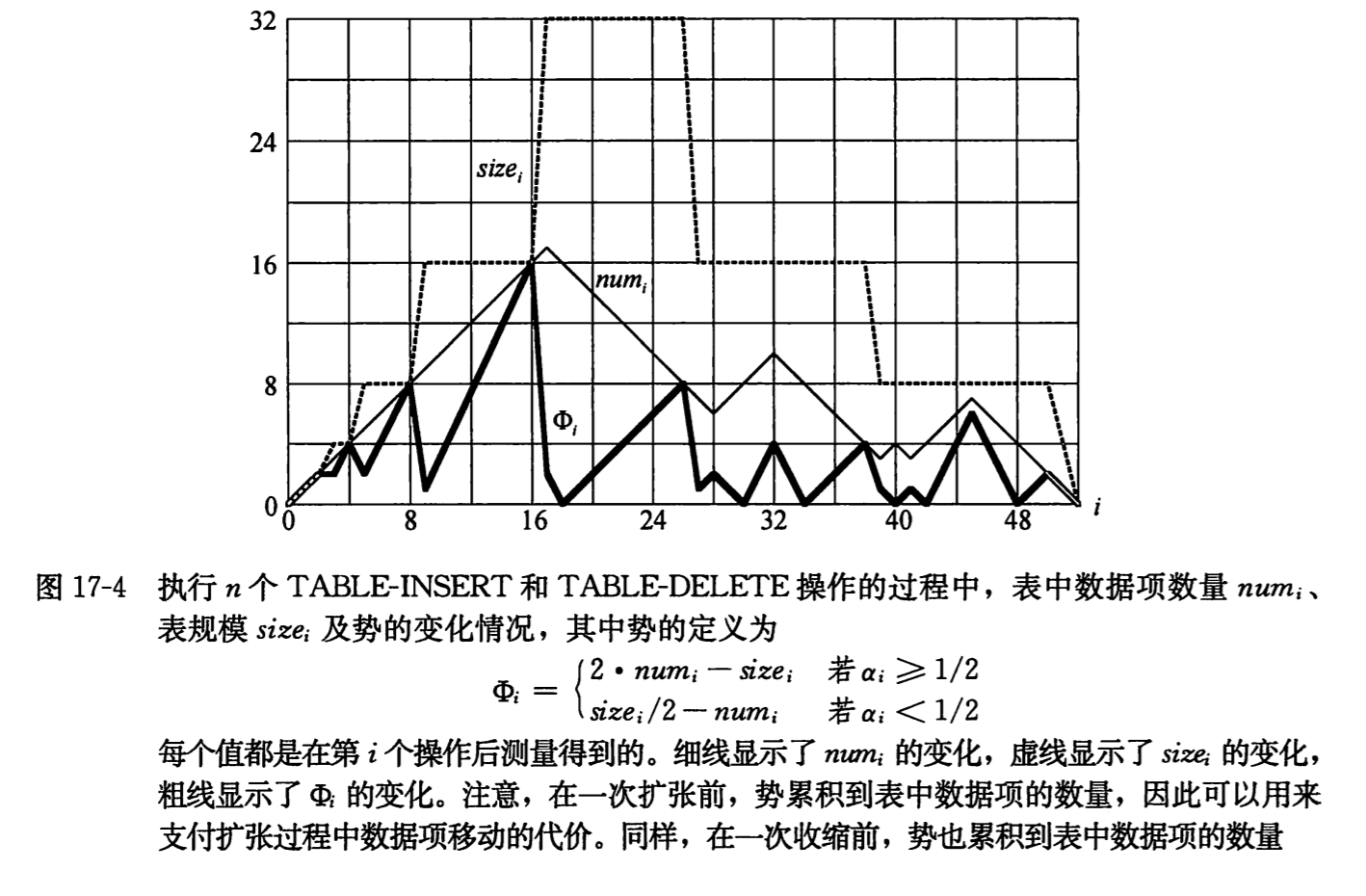
使用势能法首先分析第 i 个操作为 TABLE-INSERT 时的情况,若α(i-1) >= 1/2,分析与前文相同,无论表是否扩张摊还代价最多为 3。若α(i-1) < 1/2 且α(i) < 1/2,第 i 个操作的摊还代价为
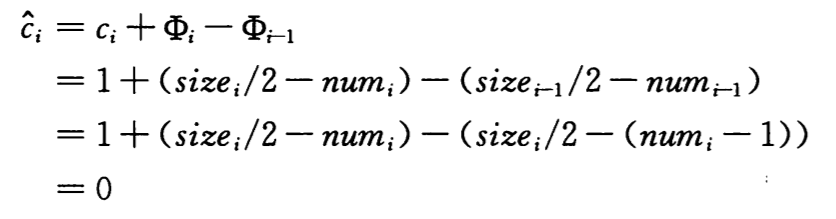
若α(i-1) < 1/2 但α(i) >= 1/2,则
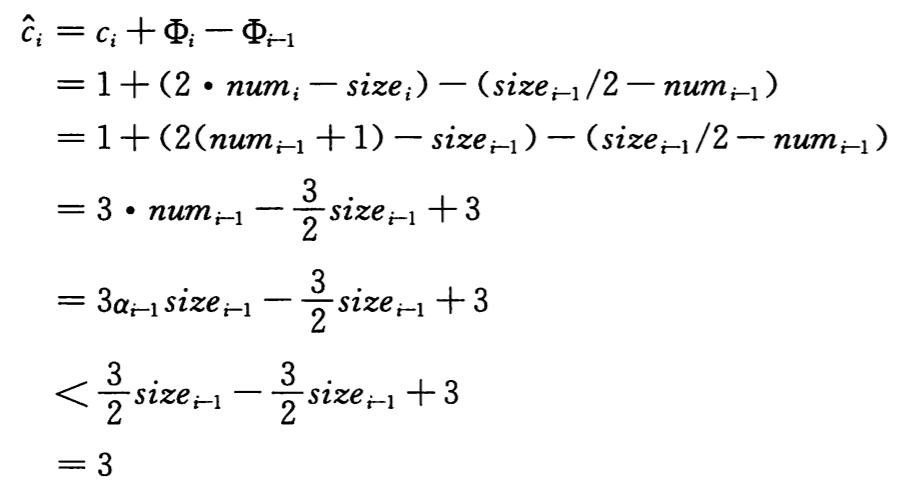
所以,一个 TABLE-INSERT 操作的摊还代价最多为 3.
接着分析第 i 个操作为 TABLE-DELETE 的情况。如果α(i-1) <1/2 且并未引起收缩,则摊还代价为
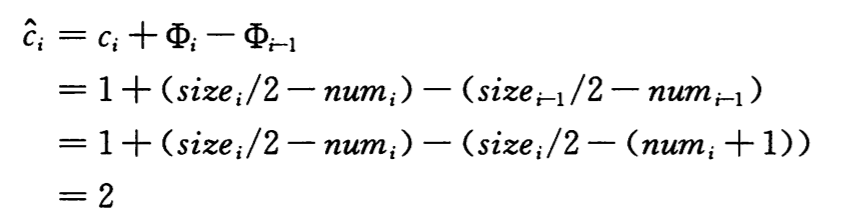
如果α(i-1) < 1/2 且第 i 个操作触发了收缩,我们有
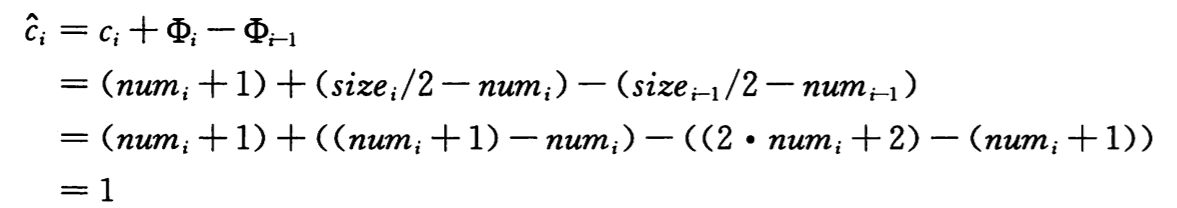
当第 i 个操作为 TABLE-DELETE 且α(i-1)时,书中将这个分析留做练习,我的算出来的答案是摊还代价为-1。
总之,每个操作的摊还代价的上界是一个常数,在一个动态表上执行任意 n 个操作的实际运行时间是Ο(n)。