红黑树

1.红黑树的性质

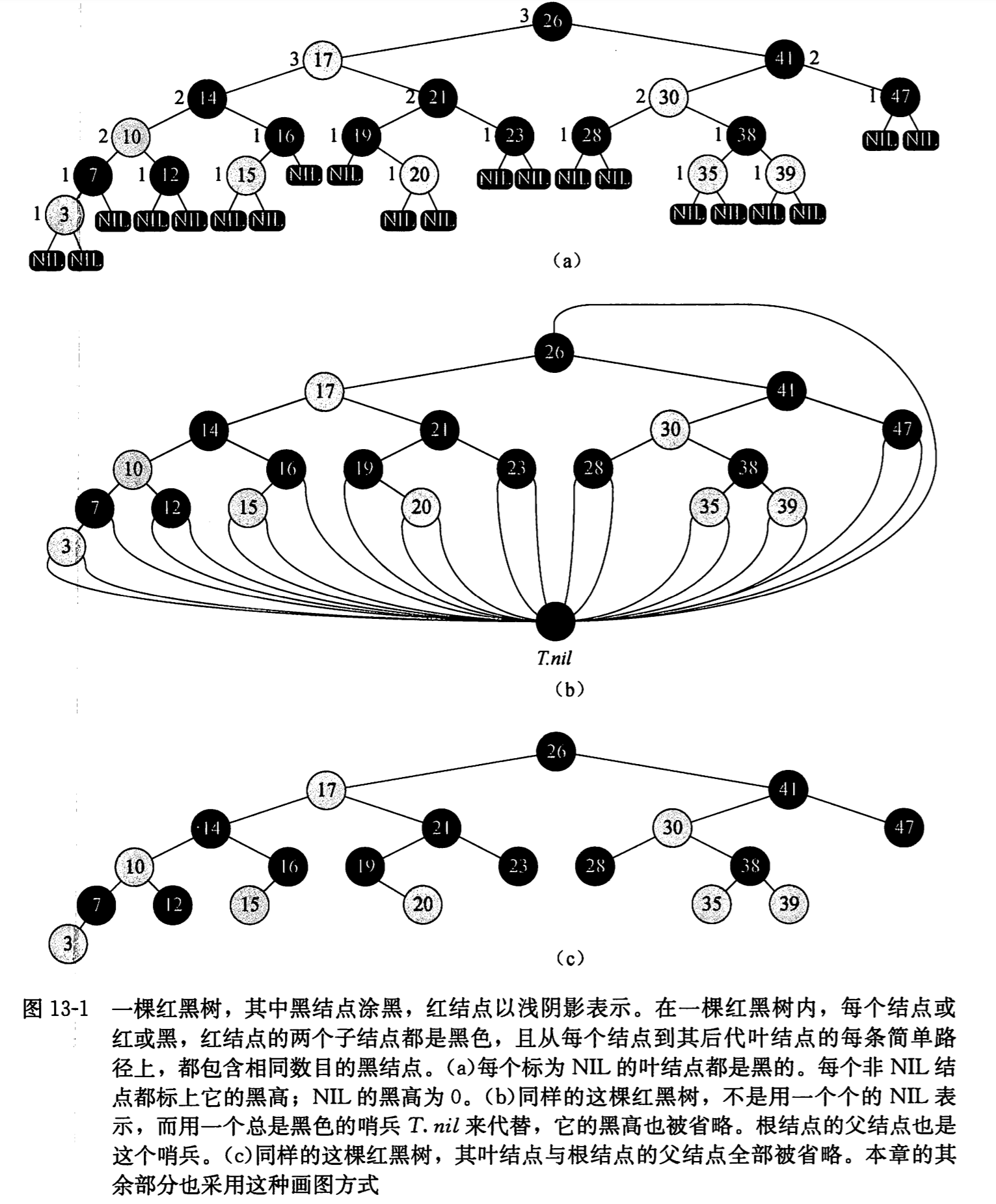
红黑树是一颗二叉搜索树，它在每个结点上增加了一个存储位来表示结点的颜色，可以是 RED 或 BLACK。通过任何一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出 2 倍，因而是近似于平衡的。

树中每个结点包含 5 个属性：color、key、left、right 和 parent。如果一个结点没有子节点或父节点，则该结点相应指针属性的值为 NIL。我们可以把这些 NIL 视为指向二叉搜索树的叶结点（外部节点）的指针，而把带关键字的结点视为树的内部节结点。

一颗红黑树是满足下面红黑性质的二叉搜索树：

每个结点或是红色的，或是黑色的。
根节点是黑色的。
每个叶结点（NIL）是黑色的。
如果一个结点是红色的，则它的两个子节点都是黑色的。
对每个结点，从该结点到其所有后代叶结点的简单路径上，均包括相同数目的黑色结点。

为了便于处理红黑树代码中的边界条件，使用一个哨兵来代表 NIL。

2.旋转

rbtree_insert 和 rbtree_delete 这两个操作对树做了修改，结果可能违反红黑性质。为了维护这些性质，必须要改变树中某些结点的颜色以及指针结构。

指针结构的修改是通过旋转(ratation)来完成的，这是一种能够保持二叉搜索性质的搜索树局部操作。

在 left_rotate 的伪代码中，假设 x.right != T.nil 且根节点的父节点为 T.nil。

    void
    left_rotate(RB_TREE *T, RB_NODE *x)
    {
        RB_NODE *y;

        y = x->right;                   //set y
        x->right = y->left;             //turn y's left subtree into x's right subtree
        if (y->left != T->nil)
            y->left->parent = x;
        y->parent = x->parent;          //link x's parent to y
        if (x->parent == T->nil)
            T->root = y;
        else if (x == x->parent->left)
            x->parent->left = y;
        else
            x->parent->right = y;
        y->left = x;                    //put x on y's left
        x->parent = y;
    }

left_rotate 和 right_rotate 操作的代码是对称的。其运行时间为Ο(1)，旋转过程中只有指针改变，其他所有属性不变。

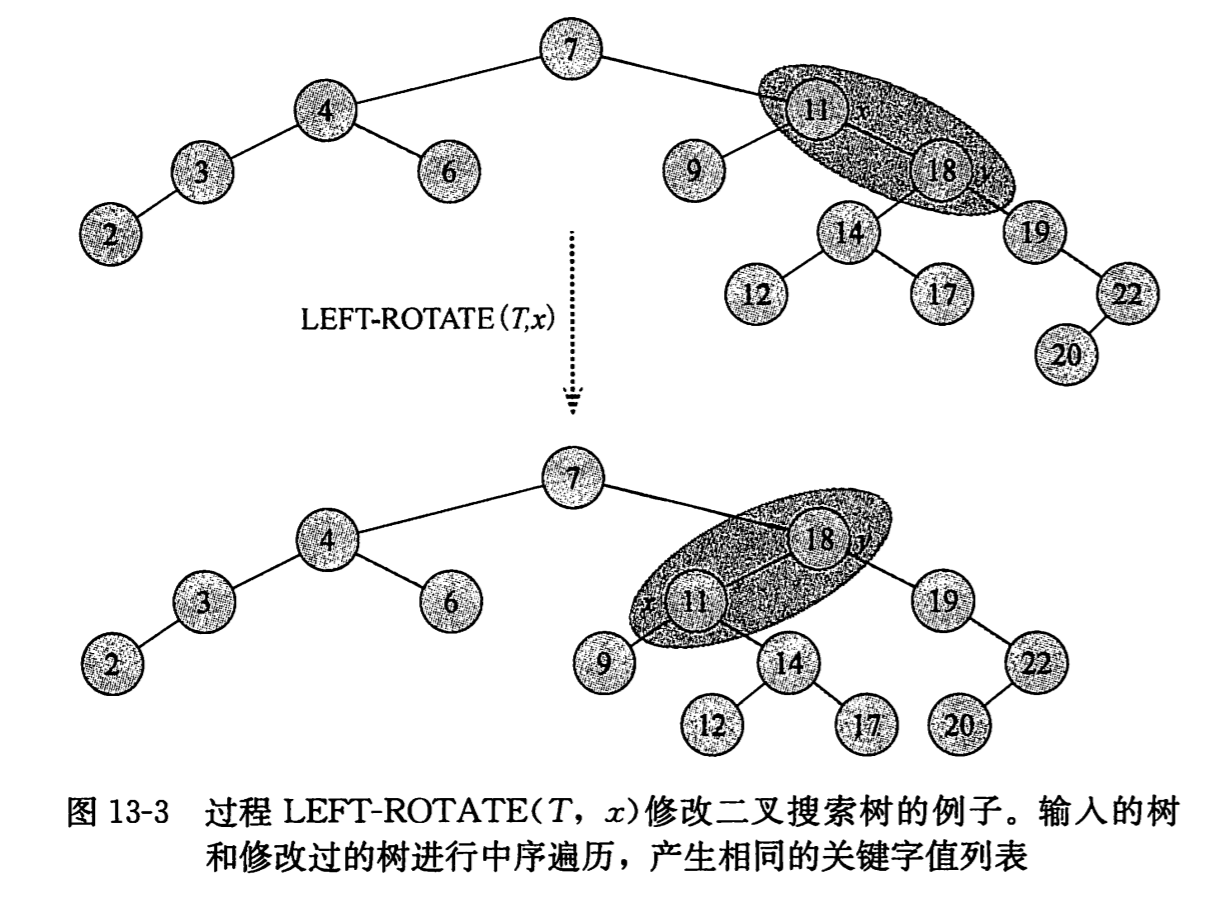
修改前和修改后的树进行中序遍历，产生相同的关键字

3.插入

我们可以在Ο(lgn)时间内完成向一颗树含 n 个结点的红黑树中插入一个新结点。将二叉搜索树的 tree_insert 略做修改来把结点 z 插入到红黑树中，就像红黑树是一颗普通的二叉搜索树，然后将 z 着为红色，并且调用一个辅助函数 rbinsert_fixup 来对结点重新着色并旋转，以保证不新插入的结点不会违反红黑性质。

    void
    rb_insert(RB_TREE *T, RB_NODE *z)
    {
        RB_NODE     *x, *y;

        y = T->nil;
        x = T->root;
        while (x != T->nil) {
            y = x;
            if (z->key &lt; x->key)
                x = x->left;
            else
                x = x->right;
        }
        z->parent = y;
        if (y == T->nil)
            T->root = z;
        else if (z->key &lt; y->key)
            y->left = z;
        else
            y->right = z;
        z->left = T->nil;
        z->right = T->nil;
        z->color = RED;
        rb_insert_fixup(T, z);
    }

    void
    rb_insert_fixup(RB_TREE *T, RB_NODE *z)
    {
        RB_NODE     *y;

        while (z->parent->color == RED) {
            if (z->parent->parent != T->nil && z->parent == z->parent->parent->left) {
                y = z->parent->parent->right;
                if (y->color == RED) {
                    z->parent->color = BLACK;           //case 1
                    y->color = BLACK;                   //case 1
                    z->parent->parent->color = RED;     //case 1
                    z = z->parent->parent;              //case 1
                    continue;                           //case 1
                }
                else if (z == z->parent->right) {
                    z = z->parent;                      //case 2
                    left_rotate(T, z);                  //case 2
                }
                z->parent->color = BLACK;               //case 3
                z->parent->parent->color = RED;         //case 3
                right_rotate(T, z->parent->parent);     //case 3
            } else {
                same as then, but exchanged &quot;right&quot; and &quot;left&quot;
            }
        T->root->color = BLACK;
        }
    }

while 循环在每次迭代的开头都保持下列 3 个部分的不变：

结点 z 是红色的。
如果 z.parent 是根结点，则它是黑色的。
如果有任何红黑性质被破坏，则最多只有一条被破坏，或是性质 2,或是性质 4。

rbinsert_fixup 操作一共可以分为三种情况，下面我们逐一进行分析：

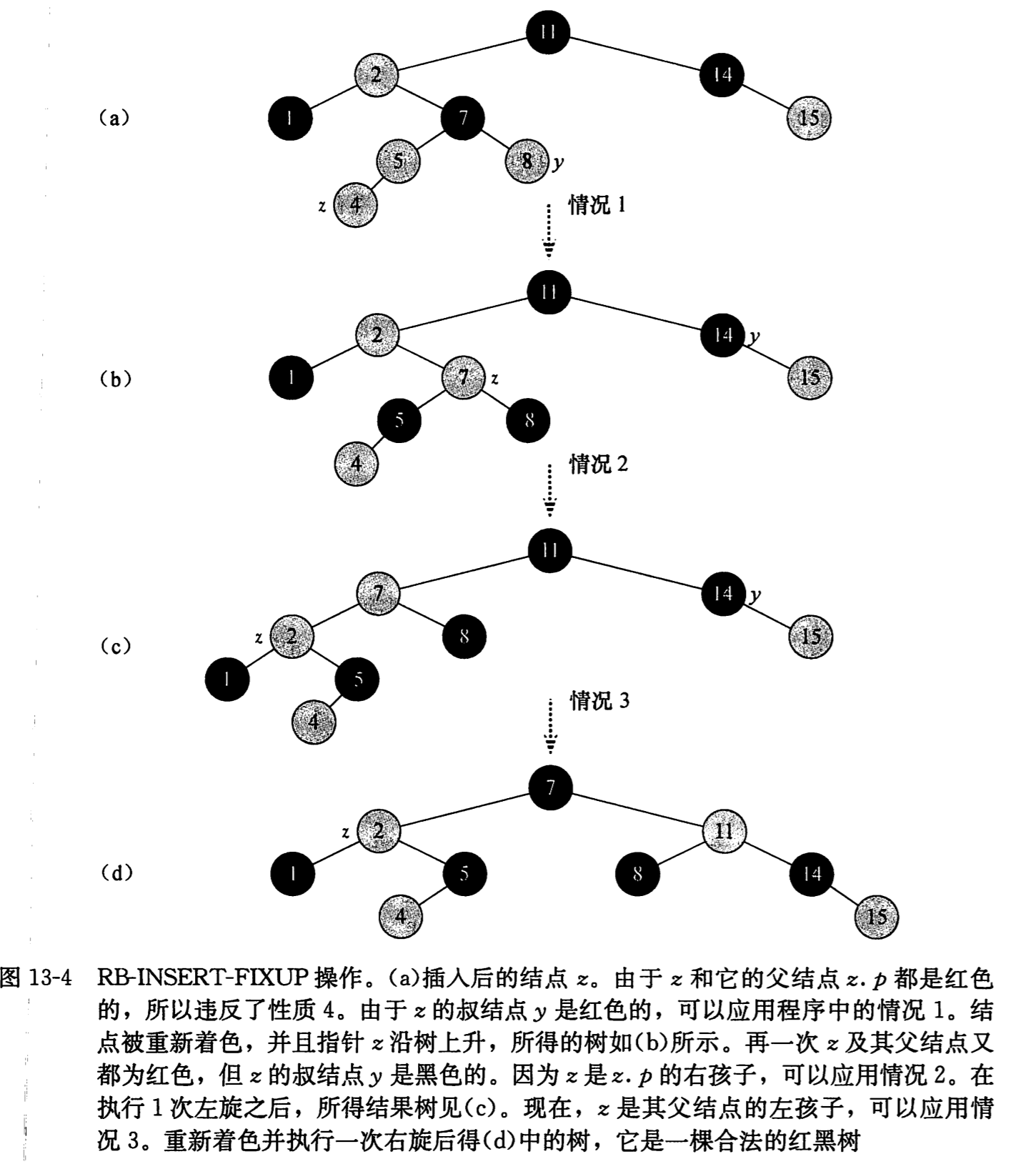
情况 1 和情况 2、3 的区别在于父亲的兄弟结点（叔结点）的颜色不同。使 y=z.parent.parent.right，然后测试 y 的颜色。如果 y 是红色的，那么执行情况 1。否则，进入情况 2、3。在所有三种情况中，z.parent.parent 的颜色都是黑色的，因为 z.parent 的颜色是红色的，所以性质 4 只在 z 和 z.parent 之间被破坏了。

情况 1：z 的叔结点 y 是红色的

这种情况在 z.parent 和 y 都是红色时发生。因为 z.parent.parent 是黑色的，所以将 z.parent 和 y 都着为黑色，来解决 z 和 z.parent 都是红色的问题，将 z.parent.parent 着为红色以保持性质 5。然后，把 z.parent.parent 作为新结点 z 来重复 while 循环。指针 z 在树中上移两层。

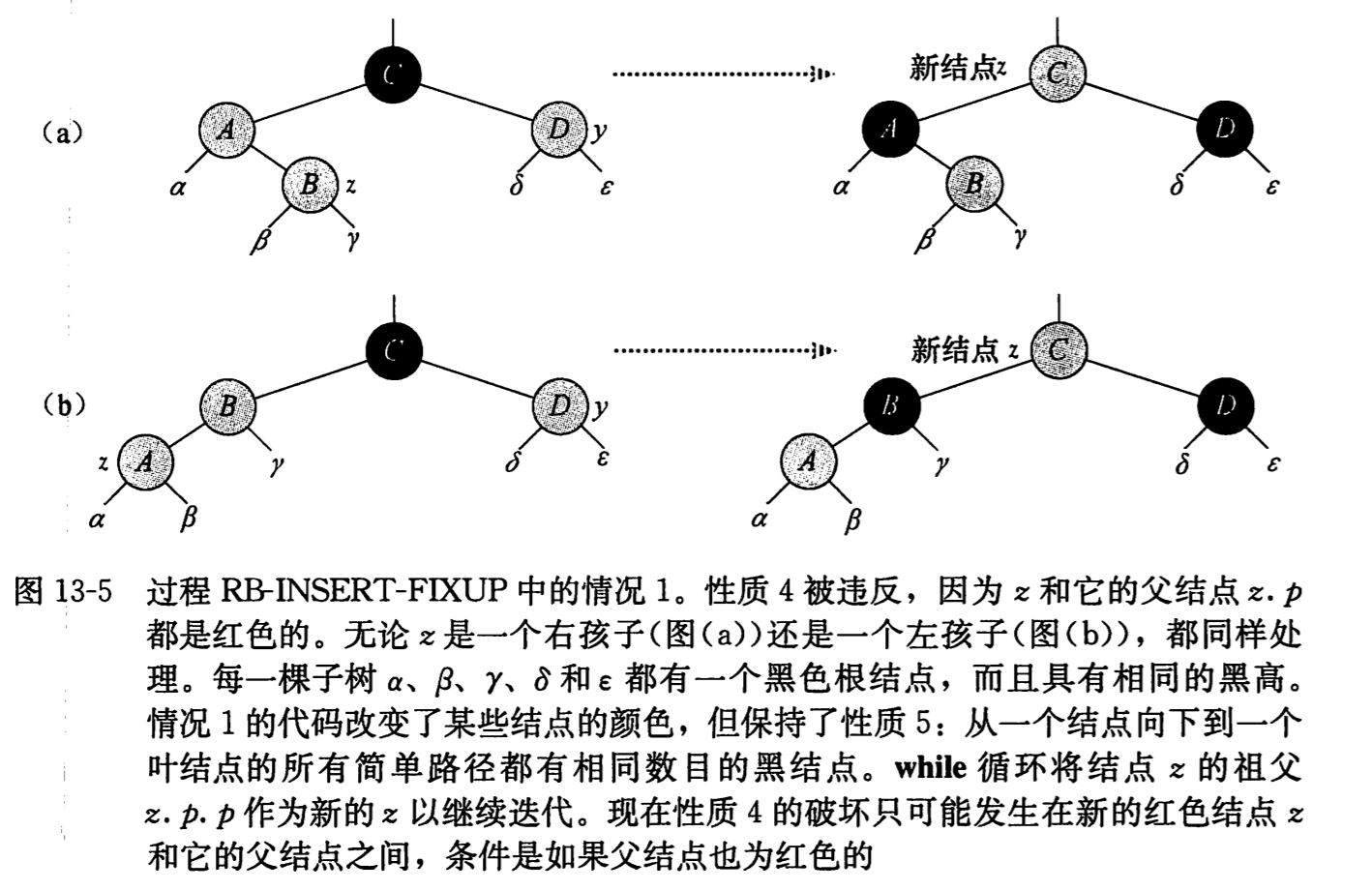
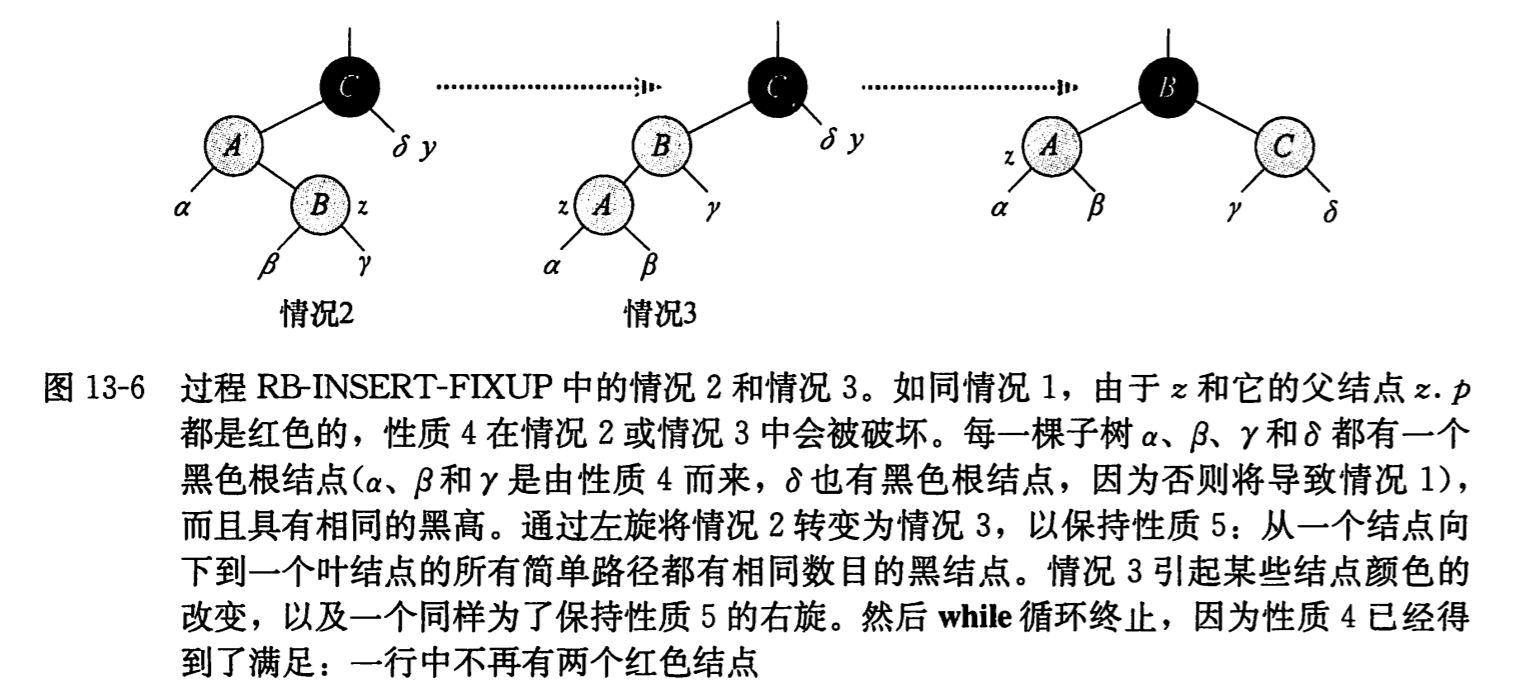
情况 2：z 的叔结点 y 是黑色的且 z 是一个右孩子

情况 3：z 的叔结点 y 是黑色的且 z 是一个左孩子

在情况 2、3 中 z 的叔结点 y 是黑色的。通过 z 是 z.parent 的右孩子还是左孩子来区分这两种情况。在情况 2 中，可以使用一个左旋来将此情况变为情况 3，结点 z 变为左孩子。因为 z 和 z.parent 都是红色的，所以这次旋转对黑高和性质 5 都没有影响。在旋转前先将 z 上移一层，然后旋转又将 z 下移了一层，z.parent.parent 的身份保持不变。在情况 3 中，改变某些节点的颜色并做一次右旋，以保持性质 5。这样，由于在一行中不再有两个红色结点，所有的处理到此完毕。另外因为此时 z.parent 是黑色的，所以无需再执行一次 while 循环。

4.删除

与红黑树的其他操作一样，删除一个结点要花费Ο(lgn)时间，但是与插入相比，删除要复杂一些。

红黑树的删除操作是基于二叉搜索树的 tree_delete 的，首先，我们需要设计一个特别的 rb_transplant 供 rb_delete 使用。

    void
    rb_transplant(RB_TREE *T, RB_NODE *u, RB_NODE *v)
    {
        if (u->parent == T->nil)
            T->root = v;
        else if (u == u->parent->left)
            u->parent->left = v;
        else
            u->parent->right = v;
        v->parent = u->parent;
    }

过程 rb_delete 和 tree_delete 类似，只是多了几行代码。多出的几行代码记录结点 y 的踪迹，y有可能导致红黑性质的破坏。当想要删除结点 z，且此时 z 的子节点少于 2 个时，直接将 z 删除，并让 y 成为 z。当 z 有两个子结点时，y应该是 z 的后继，并且 y 移到树中 z 的位置。在结点被删除或在树中移动前，必须记住 y 的颜色，并且记录结点 x 的踪迹，将 x 移到树中 y 的原来位置，因为结点 x 也可能引起红黑性质的破坏。删除结点 z 之后，rb_delete 调用一个辅助过程 rb_delete_fixup，通过改变颜色和旋转来保持红黑性质。

总结一下，z是要删除的结点，y是结点 z 的后继，是要顶替 z 原来的位置的结点，而 x 是 y 的子结点，需要 x 顶替原来的位置。

下面是 rb_delete 和 tree_delete 过程之间的其他区别：

始终维持结点 y 为从树中删除或移到树内的结点。
由于结点 y 的颜色可能改变，变量 y_original_color 存储了发生改变前的 y 的颜色。我们需要保存 y 的原始颜色，以在 rb_delete 结束时测试它，如果它是黑色的，那么删除或移动 y 会引起红黑性质的破坏。
正如前面讨论过的，我们保存结点 x 的踪迹，使它移到结点 y 的原始位置上。令 x 或指向 y 的唯一子结点或指向哨兵 T.nil（如果 y 没有子结点）。
当 y 的原父结点是 z 时，我们并不想让 x.parent 指向 y 的原父结点，因为要从树中删除该点。由于结点 y 将在树中向上移动占据 z 的位置，我们将 x.parent 设置为 y，使得 x.parent 指向 y 父结点的原始位置，甚至当 x=T.nil 时也是这样。

最后，如果结点 y 是黑色的，那么就调用 rb_delete_fixup 来恢复红黑性质。如果 y 是红色的，当 y 被删除或移动时，红黑性质仍被保持，原因如下：

树中的黑高没有变化。
不存在两个相邻的红结点。因为 y 在树中占据了 z 的位置，再考虑 z 的颜色，树中 y 的新位置不可能有两个相邻的红结点。另外，如果 y 不是 z 的右孩子，则 y 的原右孩子 x 代替 y。如果 y 是红色，则 x 一定为黑色，所以用 x 代替 y 不可能使两个红结点相邻。
如果 y 是红色的，就不可能是根结点，所以性质 2 保持。

如果结点 y 是黑色的，则会产生 3 个问题，可以通过调用 rb_delete_fixup 弥补。

如果 y 是原来的根结点，而 y 的一个红色的孩子成为新的根结点，就违反了性质 2。
如果 x 和 x.parent 是红色的，则违反了性质 4。
在树中移动 y 将导致先前包含 y 的简单路径上黑结点数目少 1。

改正这一问题的办法是将现在占据 y 原来位置的结点 x 视为还有一重额外的黑色（只是看作还有一层额外的黑色不是真的有）。也就是说，任意包含 x 的简单路径上黑结点个数加 1。在这种假设下性质 5 成立。当将黑结点 y 删除或移动时，将其黑色“下推”给结点 x。现在的问题变成了 x 可能既不是红色也不是黑色，违反了性质 1。

下面，我们将通过 rb_delete_fixup 保持红黑性质，并解决 x 既不是红色也不是黑色的问题。

    void
    rb_delete_fixup(RB_TREE *T, RB_NODE *x)
    {
        RB_NODE     *w;

        while (x != T->root && x->color == BLACK) {
            if (x == x->parent->left) {
                w = x->parent->right;
                if (w->color == RED) {
                    w->color = BLACK;                               //case 1
                    x->parent->color = RED;                         //case 1
                    left_rotate(T, x->parent);                      //case 1
                    w = x->parent->right;                           //case 1
                }

                if (w->left->color == BLACK && w->right->color == BLACK) {
                    w->color = RED;                                 //case 2
                    x = x->parent;                                  //case 2
                } else if (w->right->color == BLACK) {
                    w->left->color = BLACK;                         //case 3
                    w->color = RED;                                 //case 3
                    right_rotate(T, w);                             //case 3
                    w = x->parent->right;                           //case 3
                }
                w->color = x->parent->color;                        //case 4
                x->parent->color = BLACK;                           //case 4
                w->right->color = BLACK;                            //case 4
                left_rotate(T, x->parent);                          //case 4
                x = T->root;                                        //case 4
            } else {
                same as then, but exchanged "right" and "left"
            }
        }
        x->color = BLACK;
    }

while 循环的目标是将额外的黑色沿树上移，直到：

x 指向红黑结点，此时在最后，将 x 着为（单个）黑色。
x 指向根结点，此时可以简单地“移除”额外的黑色。
执行适当的旋转和重新着色，退出循环。

在 while 循环中，x总是指向一个具有双重黑色的非根结点。并保持 w 指向 x 的兄弟。由于 x 是双重黑色的，所以 w 不可能是 T.nil，否则 x.parent 到 w 的简单路径上的黑结点数目就会少于 x.parent 到 x 的简单路径上的黑结点数目。

rb_delete_fixup 的关键思想是在每种情况中，从子树的根到每棵字数α，β，……，ζ之间的黑结点个数（包括 x 的额外黑色）并不改变。

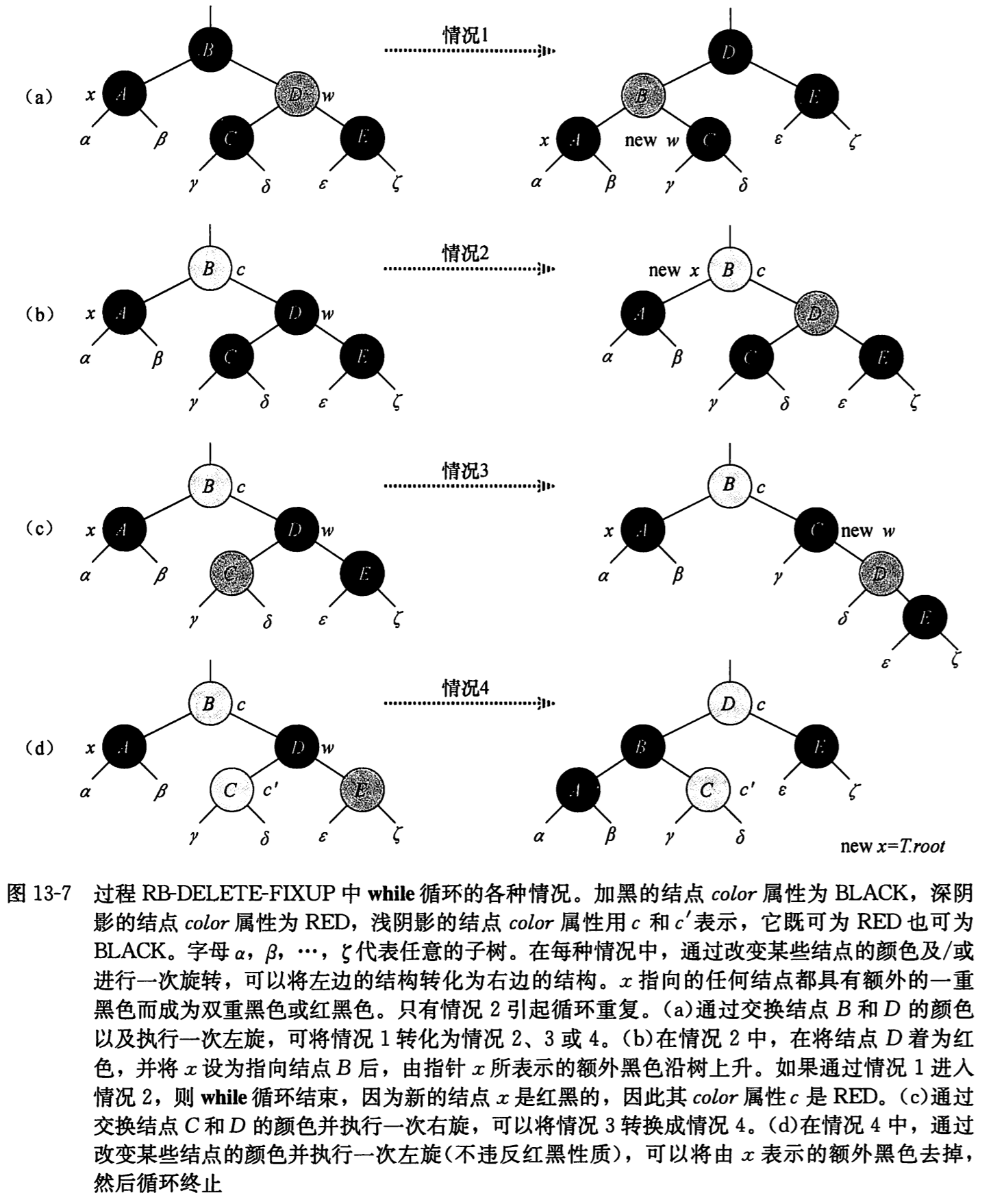
加黑的结点颜色为 BLACK，深阴影的结点颜色为 RED，浅阴影的结点颜色用 c 和 c'表示，既可以为红色也可以为黑色。

情况 1：x 的兄弟结点 w 是红色的

因为 w 必须有黑色子结点，所以可以改变 w 和 x.parent 的颜色，然后对 x.parent 做一次左旋而不违背红黑性质。现在，x的新兄弟结点是旋转前 w 的某个子结点，其颜色为黑色。这样就把情况 1 转换为了情况 2、3、4。

当结点 w 为黑色时，属于情况 2、3 和 4 这些情况是由 w 的子结点的颜色来区分的。

情况 2：x 的兄弟结点 w 为黑色，且 w 的两个子结点都是黑色

因为 w 也是黑色的，所以从 x 和 w 上去掉一重黑色，使得 x 只有一重黑色而 w 为红色。为了补偿从 x 和 w 中去掉的黑色，在原来的 x.parent 上新增一重额外额黑色。通过将 x.parent 作为新的 x 来重复 while 循环。

情况 3：x 的兄弟结点 w 为黑色，且 w 的左孩子为红色，右孩子为黑色

可以交换 w 和其左孩子 w.left 的颜色，然后对 w 进行右旋。现在 x 新的兄弟结点 w 是一个有红色右孩子的黑色结点，于是情况 3 就变成了情况 4。

情况 4：x 的兄弟结点 w 为黑色，且 w 的右孩子为红色

通过进行某些颜色修改并对 x.parent 做一次左旋，可以去掉 x 的额外黑色，从而使它变为单重黑色，而不破坏红黑性质。之后再将 x 设置为根，退出 while 循环。

通过以上 4 中情况的循环，我们可以将 x 的额外黑色消除，从而在不违背任何红黑性质的情况下删除一个结点。

红黑树

目录