贪心算法原理

第一个关键要素是 贪心选择性质 ：我们可以通过做出局部最优选择来构造全局最优解。换句话说，在进行选择的时候，直接做出在当前问题中看起来最优的选择，而不必考虑子问题的解。

当然，我们必须证明每个步骤做出贪心选择能生成全局最优解。这种证明通常首先考察某个子问题的最优解，然后用贪心选择替换某个其他选择来修改此解，从而得到一个相似但是更小的子问题。如果在进行贪心选择的时候不得不考虑众多选择，通常意味着可以改进贪心选择，使其更为高效。

最优子结构 性质是能否应用动态规划和贪心算法的关键要素。比起动态规划而言，贪心算法通常使用更为直接的最优子结构。假定通过对原问题进行贪心选择就可以得到子问题。我们真正要做的全部工作就是论证：将子问题的最优解与贪心选择组合在一起能生成原问题的最优解。这种方法隐含地对子问题使用了数学归纳法，证明了在每个步骤进行贪心选择会生成原问题的最优解。

由于贪心算法和动态规划都使用了最优子结构性质，你可能会对一个可用贪心算法求解的问题使用动态规划，或者相反。为了说明这两种方法之间的微妙差别，我们研究一个经典最优化问题的两个变形。

0-1 背包问题 ：一个正在抢劫商店的小偷发现了 n 个商品，第 i 个商品价值 vi 元，重 wi 磅，vi 和 wi 都是整数。小偷希望拿走价值尽可能高的商品，但是背包最做只能容纳 W 磅。他应该拿走哪些商品呢？

分数背包问题 ：设定与 0-1 背包一样，但是对每个商品，小偷可以只拿走其一部分，而不是只能做出二元(0-1)选择。可以把 0-1 背包问题中的商品看做品质不一大小不同的金块，而分数背包问题中的商品更像是金砂。

两个问题都具有最优子结构性质，虽然两个问题相似，但是我们可以用贪心算法求解分数背包，而不能求解 0-1 背包。为了求解分数背包，我们先计算每个商品的价重比即 vi/wi。遵循贪心选择，先尽可能的拿走价重比最高的商品，如果此商品全部都拿走了，再继续拿价重比第二高的商品，依次类推，直到背包装满为止。

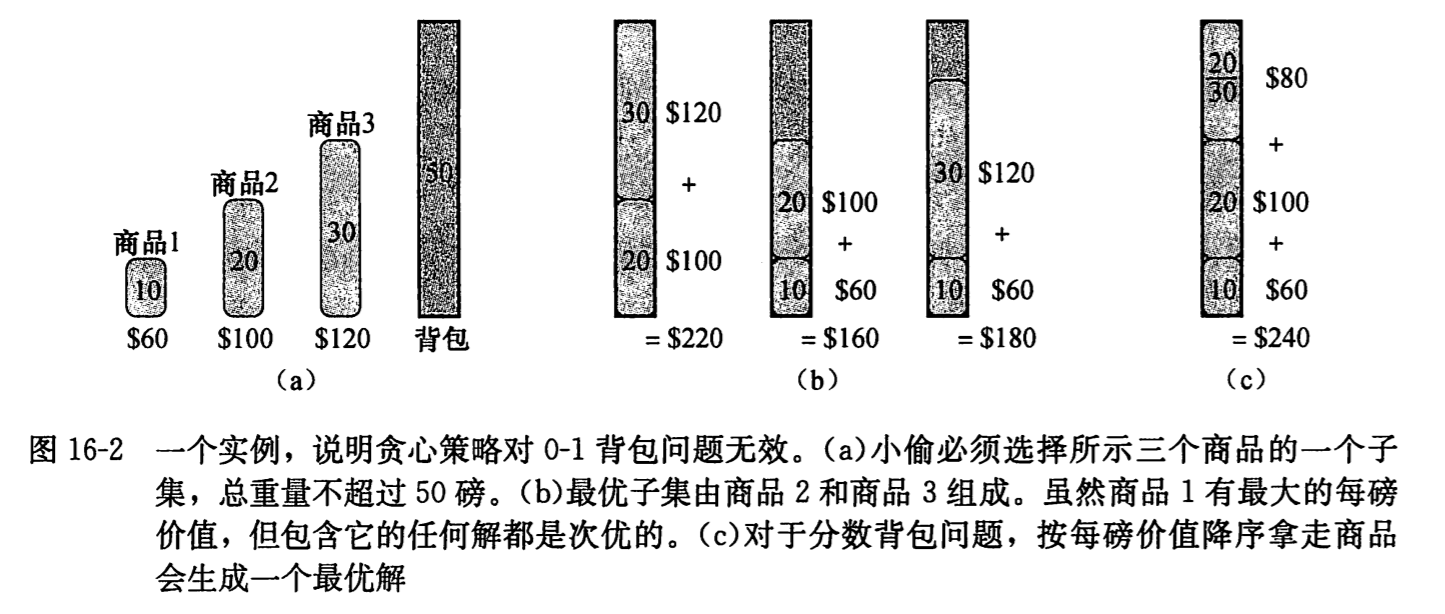
为了说明贪心策略对 0-1 背包问题无效，我们使用下图中实例。商品的价格在最下，而用长度来表示商品的重量和背包的最大容量 W，即 50。按照贪心算法，小偷应先拿走商品 1，但是如下图(b)所示，最优解应该是拿走商品 2 和商品 3。

但是对于分数背包问题，如(c)所示先拿走商品 1 是可以生成最优解的。拿走商品 1 对 0-1 背包问题无效是因为小偷无法装满背包，空闲空间降低了方案的有效价重比。在 0-1 背包问题中，当考虑是否将一个商品装入背包时，必须比较包含此商品的子问题的解与不包含它的子问题的解，然后才能做出选择。这会导致大量的重叠子问题——动态规划的标识。