贪心算法：活动选择

采用动态规划求解最优化问题时，需要经过一系列的步骤，并且在每个步骤都面临多种选择，这对许多最优化问题来说有杀鸡用牛刀了，可以使用更加简单、高效的算法。*贪心算法*就是这样的算法，在每一步都选择当时看起来的最优解，总是作出局部最优的选择，从而希望能够得到一个全局最优解。贪心算法不保证能够得到最优解，但是对许多问题的确可以得到最优解。贪心算法是一种强有力的算法，可以很好地解决很多问题。下面通过一个活动选择例子来直观了解一下贪心算法。

活动选择问题

假设有一个包含 n 个活动的集合 S = {a1, a2, …, an}，这些活动使用同一个资源（如同一个教室），而这个资源在同一时刻只能由一个活动使用。每个活动 ai 都有一个开始时间 s1 和结束时间 f1，也就是说一个活动的半开时间为[si, fi)。如果两个活动 ai 和 aj 的半开时间区间是不重叠的，则称它们是兼容的。 活动选择问题 就是希望选出一个最大兼容活动集。假设活动已按结束时间单调递增顺序排序。则一个活动集合 S 如下：

活动选择1.png

活动选择问题的最优子结构

令 S(ij)表示在 ai 结束之后开始，且在 aj 开始之前结束的活动集合。我们需要求 S(ij)的一个最大互相兼容的活动子集，假设 A(ij)就是这样的子集，包含活动 ak。由于最优解包含活动 ak，我们得到两个子问题：寻找 S(ik)中的兼容活动和寻找 S(kj)中的兼容活动。因此，有 A(ij) = A(ik) ∪ {ak} ∪ A(kj)，S(ij)中最大兼容活动子集 A(ij)包含|A(ik)|+|A(kj)|+1 个活动。

令 C[i, j]表示合计 S(ij)的最优解大小，遍历考察 ak 的最优选择，则可以得到递归式：

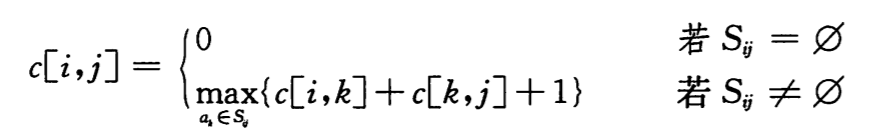
活动选择2.png

贪心选择

其实，对于活动选择问题，我们不必考察所有可能的选择就可解决问题，即只考虑一个选择：贪心选择。

直观上，贪心选择就是选择这样一个任务，选出它后剩下的资源能够被尽量多的其他任务所用。对于活动选择问题来说，贪心选择其实就是选择 S 中最早结束的活动，即 a1。不过选择最早结束的活动并不是活动选择问题唯一的贪心选择方法。令 Sk 为在 ak 结束后开始的活动集合，当做出了贪心选择 a1 后，剩下的 S1 就成了唯一需要求解的子问题。相比动态规划需要求解两个子问题来说，贪心选择更加简单、高效。另外，贪心算法通常都是自顶向下的设计：做出一个选择，然后求解剩下的那个子问题，而不是自底向上地求解出很多子问题，然后再做出选择。

递归贪心算法

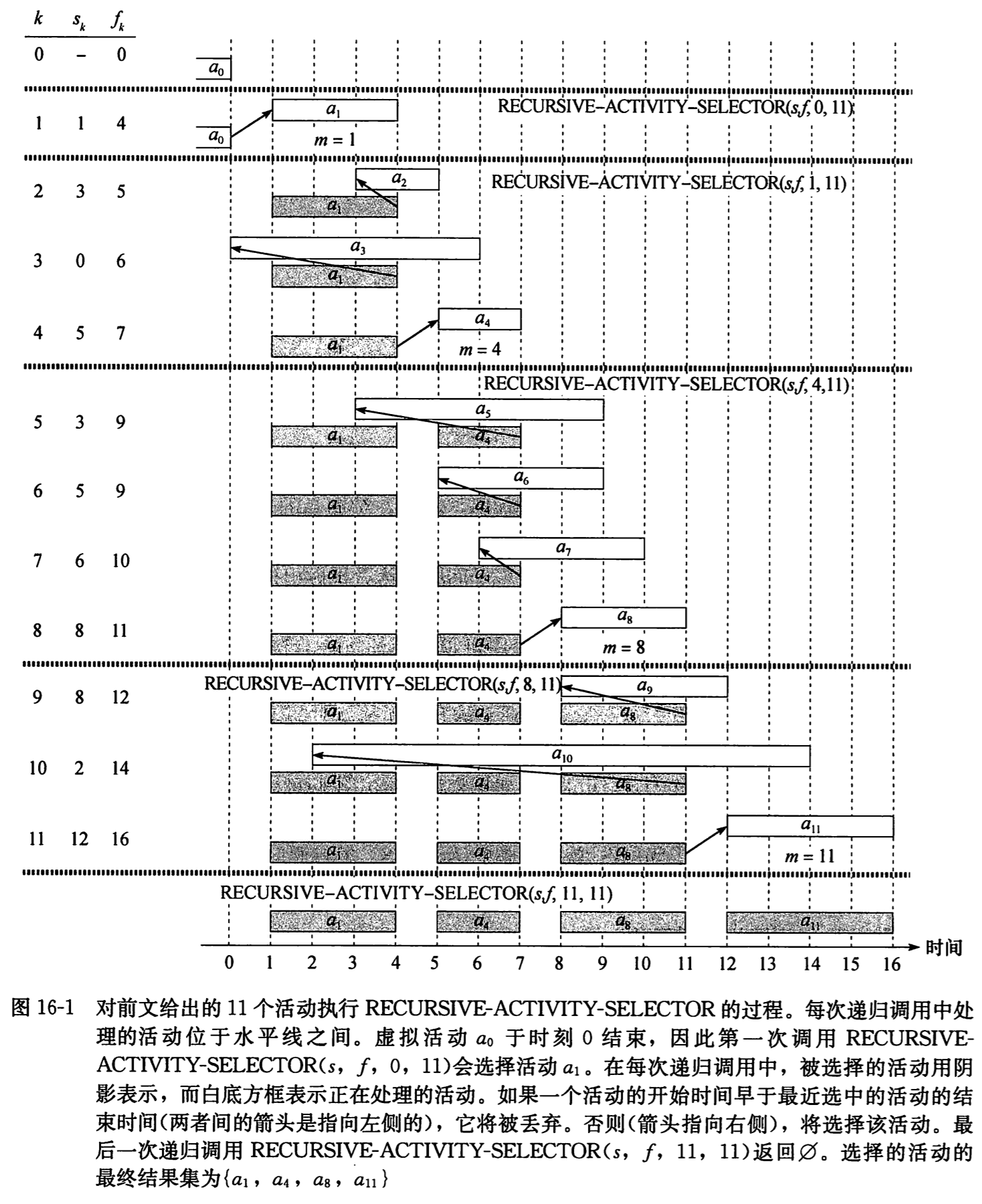
过程 recursive_activity_selector 的输入为两个数组 s 和 f，分别是活动的开始和结束时间，k指出要求解的子问题 Sk，n 为问题规模，它返回 Sk 的一个最大兼容活动子集并保存在 a 中。为了方便求解，假设输入的 n 个活动都已经按结束时间的单调递增顺序排列好，如果没有排好序，我们也可以在Ο(nlgn)时间内对其进行排序。另外为了方便算法初始化，还添加了一个虚拟活动 a0，其结束时间为 f0 = 0。这样子问题 S0 就是完整的活动集 S。具体算法见下文 C 语言代码，也加了几行简单的注释。如下图所示，其核心思想只是简单的选择第一个在活动 ak 结束之后开始的活动。

活动选择3.png

迭代贪心算法

很好理解，没有什么好说的，详细信息见下文代码。

C 语言实现代码

    #include <stdlib.h>
    #include <stdio.h>
    #include <string.h>

    #define N       11
    #define MAXBUF  20

    void
    recursive_activity_selector(int *s, int *f, int k, int n , char *a)
    {
        int     m;
        char    buf[4];

        m = k + 1;
        while (m <= n && s[m] < f[k])
            /*
             * 跳过开始时间在f[k]之前的活动
             */
            m = m + 1;
        if (m <= n) {
            /*
             * 贪心选择，找到开始时间在f[k]之后的第一个活动后，
             * 直接把它加入到活动列表中
             */
            sprintf(buf, "a%d ", m);
            strcat(a, buf);
            recursive_activity_selector(s, f, m, n, a);
        }
    }

    void
    greedy_activity_selector(int *s, int *f, char *a)
    {
        int     k, n, m;
        char    buf[4];

        strcat(a, "a1 ");
        n = N;
        k = 1;

        for (m = 2; m <= n; m++) {
            if (s[m] >= f[k]) {
                sprintf(buf, "a%d ", m);
                strcat(a, buf);
                k = m;
            }
        }
    }

    int
    main(int argc, const char *argv[])
    {
        int     s[N + 1] = {0, 1, 3, 0, 5, 3, 5,  6,  8,  8,  2, 12};
        int     f[N + 1] = {0, 4, 5, 6, 7, 9, 9, 10, 11, 12, 14, 16};
        char    a[MAXBUF] = "";

        /* recursive_activity_selector(s, f, 0, N, a); */
        greedy_activity_selector(s, f, a);

        printf("%s", a);

        return 0;
    }