数据结构的扩张

一些工程应用需要的只是一些”教科书“中的标准数据结构，然而也有需要其他的应用需要对现有的数据结构进行少许的创新和改造，不过很少需要创造出一类全新的数据结构。更经常的是，通过存储额外信息的方法来扩张一种标准的数据结构，然后编写新的操作来支持所需要的应用。但是对数据结构的扩张并不是简单直接的，因为添加的信息必须要能被该数据结构上的常规操作更新和维护。

下面介绍了两种红黑树扩张出的两种数据结构，和扩张数据结构的一般方法。

1.动态顺序统计

顺序统计树是一种支持快速顺序统计的数据结构，它只是简单地在每个结点上存储附加信息的一颗红黑树。在结点 x 中除了一般的结点属性之外还包括一个 x.size 属性，它包含了以 x 为根的子树还有 x 本书的结点数，即这颗子树的大小。（哨兵的 size 属性为 0）

x.size = x.left.size + y.right.size + 1

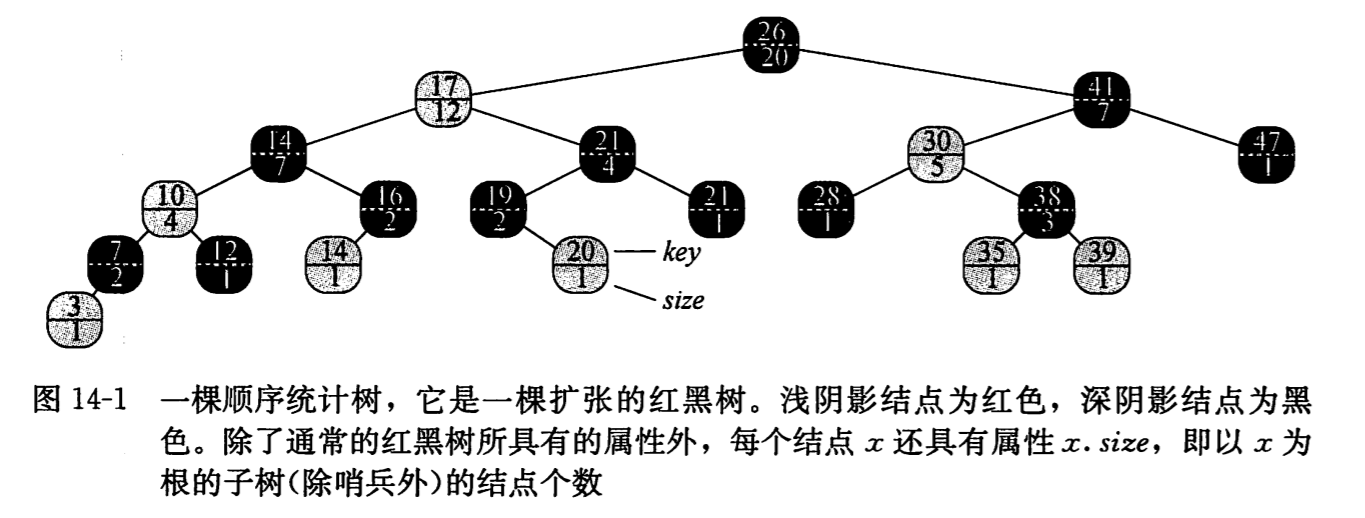
顺序统计树.png

查找具有给定秩的元素

在说明如何在插入和删除中维护 size 属性前，我们先来看看可以利用 size 属性实现的功能。第一是查找具有给定秩的元素。我们定义一个元素的秩为在中序遍历时其输出的位置。

过程 os_select(x, i)，返回一个指向以 x 为根的子树包含第 i 小关键字的结点。

    RB_NODE *
    os_select(RB_NODE *x, int i)
    {
        /*
        * return ith small element in tree.
        */
        int     r;

        r = x->left->size + 1;
        if (i == r)
            return(x);
        else if (i < r)
            return(os_select(x->left, i));
        else
            return(os_select(x->right, i - r));
    }

其核心思想很简单，x.left.size + 1 就是以 x 为根的子树中结点 x 的秩。如果 i = r，那么 x 就是第 i 小元素，如果 i < r，那么第 i 小元素就在 x 的左子树中，如果 i > r，那么第 i 小元素在 x 的右子树中。因为以 x 为根的子树进行中序遍历时，有 r 个元素排在 x 的右子树之前，所以在以 x.right 为根进行递归 i 调用时，第 i 小元素就变成了第 i – r 小元素。

因为每次递归都在树中下降一层，所以 os_select 的运行时间与树的高度成正比，又因为它是一颗红黑树，所以 os\_select 运行时间为Ο(lgn)。

确定一个元素的秩

给定一个元素，过程 os_rank 返回这个元素的秩。

    int
    os_rank(RB_TREE *T, RB_NODE *x)
    {
        /*
        * return x's rank in inorder_tree_walk.
        */
        int         r;
        RB_NODE     *y;

        r = x->left->size + 1;
        y = x;

        while (y != T->root) {
            if (y == y->parent->right)
            r = r + y->parent->left->size + 1;
            y = y->parent;
        }

        return(r);
    }

x 的秩是中序遍历次序排在 x 之前的结点数再加上 1。如果 x 是其父结点的右孩子，说明 x.parent.left 是排在 x 之前的结点。while 循环中 y 在树中上升一层，直到根为止，依次遍历了排在 x 之前的结点，然后将在 while 循环中遇到的排在 x 之前的结点数累加起来，最后得到 x 的秩并返回。

对子树规模的维护

下面我们来看看如何对修改后的红黑树进行维护。

由红黑树的理论可知，红黑树上的插入操作包括两个阶段。第一阶段从根开始沿树下降，将新节点插入作为某个已存在结点的孩子。第二阶段沿树上升，做一些变色和旋转操作来保持红黑树性质。

对第一阶段的维护没有采用算法导论中的方法，没想明白书中的“对由根至叶子的路径上遍历的每一个结点 x，都增加 x.size 属性。新增加结点的 size 为 1。”是怎么可能实现对红黑树的维护的……

我的方法是从插入的结点开始到根为止，遍历这条路径上的每一个结点，并使用一开始介绍的公式维护其 size 属性，正好删除的时候也要使用这个方法，一举两得。

    void
    os_fixwalk(RB_TREE *T, RB_NODE *x)
    {
        RB_NODE *y;

        y = x;

        while (y != T->root) {
            y->size = y->left->size + y->right->size + 1;
            y = y->parent;
        }
    }

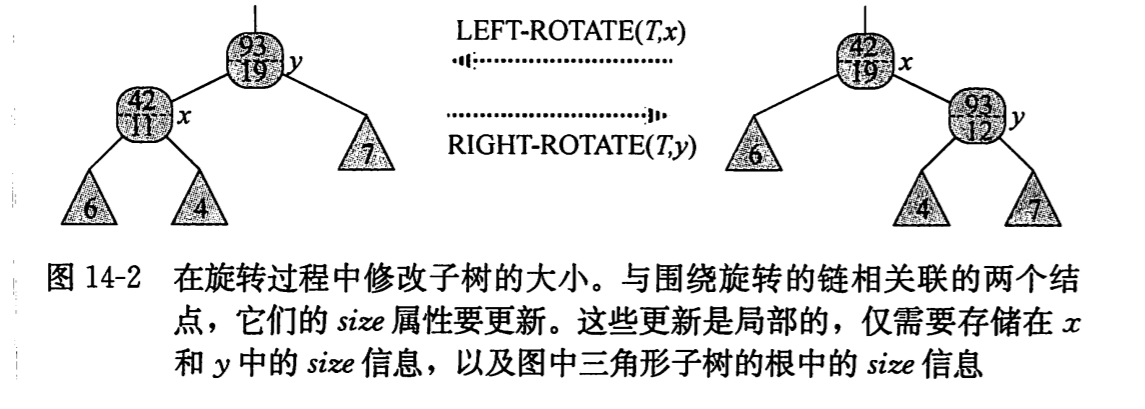
在第二阶段，对红黑树结构上的改变仅仅是由旋转所致，它会使两个结点的 size 属性失效，只要在 left\_rotate 和 right\_rotate 中简单的增加两行就可以对失效的 size 属性进行更新。

    /* left_rotate */
    y->size = x->size;
    x->size = x->left->size + x->right->size + 1;

    /*right_rotate */
    x->size = y->size;
    y->size = y->left->size + y->right->size + 1;

对树子规模的维护.png

红黑树上的删除操作也包括两个阶段：第一阶段中，要么将结点 y 从树中删除，要么将它在树中上移。为了更新子树的规模，我们只需要遍历一条由结点 y（从它在书中的原始位置开始）到根的简单路径，并减少路径上每个结点的 size 属性值，使用的还是上面的 os\_fixwalk 过程。第二阶段最多做三次旋转，其他对结构没有影响。

2.如果扩张数据结构

对基本的数据结构进行扩张以支持一些附加功能，在算法设计过程中是相当常见的。

扩张一种数据结构可以分为 4 个步骤：

选择一种基础数据结构。
确定基础数据结构中要维护的附加信息。
检验基础数据结构上的基本修改操作能否维护附加信息。
设计一些新操作

以上仅作为一个一般模式，不应盲目地按照上面给定的次序来执行这些步骤。大多数的设计工作都包含试探和纠错的成分，过程中的所有步骤通常都可以并行执行。

设计顺序统计树时，就依照了这 4 个步骤。

步骤 1，选择了红黑树作为基础数据结构。

步骤 2，添加了 size 属性，附加信息可使各种操作更加有效。有了 size 属性，我们可以在Ο(lgn)时间内完成 os\_select 和 os\_rank。

步骤 3，保证了插入和删除操作仍能在Ο(lgn)时间内维护 size 属性。比较理想的是，只需要更新该数据结构中的几个元素就可以维护附加信息。

步骤 4，设计了新操作 os\_select 和 os\_rank。归根结底，一开始考虑去扩张一个数据结构的原因就是为了满足新操作的需要。然后有时并不是为了设计一些新操作，而是利用附加信息来加速已有的操作。

3.区间树

区间便于表示占用一连续时间段的一些事件。例如，查询一个由时间区间数据构成的数据库，去找出给定时间区间内发生了什么时间。

这里所有的区间都是闭区间，我们可以把一个区间表示为一个对象 i，其中属性 i.low 为低端点，i.high 为高端点，任何两个区间 i 和 i'都满足区间三分律，即下面三条性质之一成立：

i 和 i'重叠
i 在 i'的左边
i 在 i'的右边

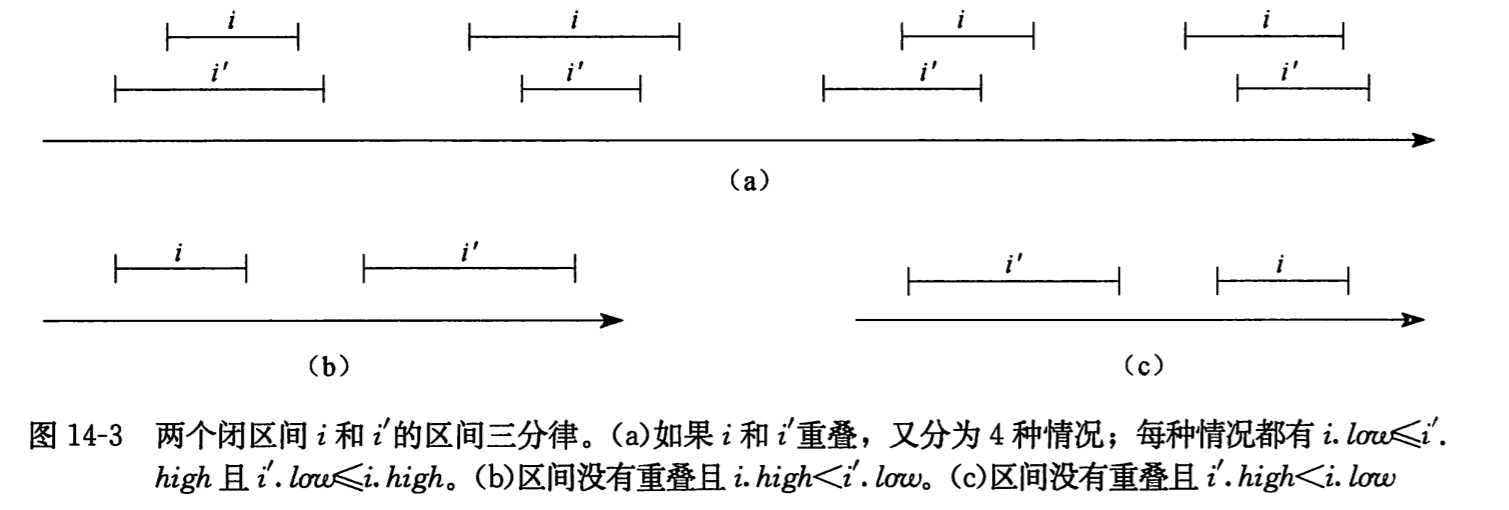
区间树1.png

(a)i 和 j 重叠的四种情况。(b)i 在 i'的左边。(c)i 在 i‘的右边。

区间树是一种对动态集合维护的红黑树，其中每个元素 x 都包含一个区间 x.int。我们将按照第 2 节中的 4 个步骤，来分析区间树以及区间树上各种操作的设计。

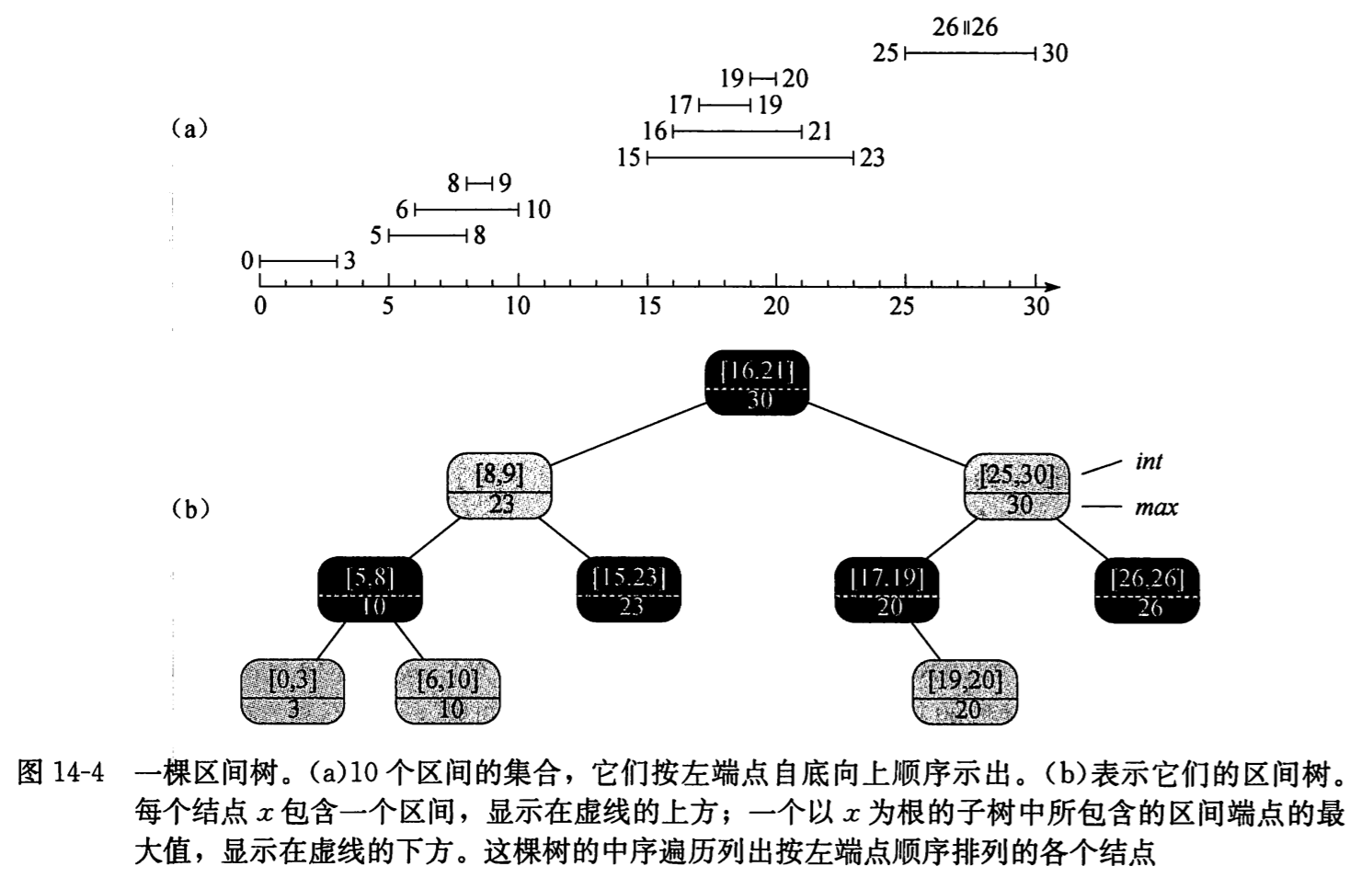
区间树2.png

(a)10 个区间的集合，按低端点自底向上顺序。(b)表示它们的区间树。其中序遍历列出按低端点顺序排列的结点。

步骤 1：数据数据结构

选择一颗红黑树，其每个结点 x 包含一个区间属性 x.int，且 x 的关键字为区间的低端见 x.int.low。

步骤 2：附加信息

每个结点除了区间属性外，还包含一个值 x.max，它是以 x 为根的子树中所有区间的端点的最大值。

步骤 3：对信息的维护

验证 n 个结点的区间树上的插入和删除操作能否在Ο(lgn)内完成。通过给定的区间和子结点的 max 值，可以确定该结点的 max 值。

x.max = max(x.int.high, x.left.max, x.right.max)

维护过程与顺序统计树类似，这里不再重复叙述。

步骤 4：设计新的操作

interval_search 用来找出树 T 中与区间 i 重叠的那个结点。

    RB_NODE *
    interval_search(RB_TREE *T, INT i)
    {
        RB_NODE *x;
        x = T->root;

        while (x != T->nil && !overlap(x->inv, i)) {
            if (x->left != T->nil && x->left->max >= i.low)
                x = x->left;
            else
                x = x->right;
            }
        return(x);
        }

        int
        overlap(INT x, INT y)
        {
            if (x.high < y.low || x.low > y.high)
                return(0);
            else
                return(1);
        }
    }

该过程的基本思想是在任意结点 x 上，如果 x.int 不与 i 重叠，则查找总是沿着一个安全的方向进行。