摊还分析
先来直观的介绍一下什么是 摊还分析 :在摊还分析中,我们求数据结构的一个操作序列中所执行的所有操作的平均时间,来评价操作的代价。这样,我们就可以说明一个操作的平均代价是很低的,即使序列中某个单一操作的代价很高。摊还分析不同于平均情况分析,它不涉及概率,它可以保证/最坏情况下每个操作的平均性能/。
在学习摊还分析的时候要注意,在摊还分析中赋予对象的费用仅仅是用来分析而已,不需要也不应该出现在程序中。通过做瘫痪分析,通常可以获得对某种特定数据结构的认识,这种认识有助于优化设计。
聚合分析
使用 聚合分析 ,我们可以证明对所有 n,一个 n 个操作的序列最坏情况下花费的总时间为 T(n)。因此,在最坏情况下,每个操作的平均时间,或 摊还代价 为 T(n)/n。注意,此摊还代价是适用于每个操作的,即使序列中有多种类型操作。下面通过两个例子来了解一下聚合分析。
栈操作
经典的栈操作,这里不过多叙述,它支持三种操作:
- PUSH(S, x),压入对象 x。
- POP(S),弹出一个对象。
- MULTIPOP(S, k),弹出 k 个对象,如果栈中对象的数量少于 k,则将所有对象弹出。
我们来分析一下 n 个这三种操作在一个空栈上的运行时间。一个 MULTIPOP 操作的最坏情况时间为О(n),因为栈的大小为最大为 n,PUSH 和 POP 最坏情况时间均为 1,假设序列中的有О(n)个 MULTIPOP 操作,所以我们通过分析每个操作的最坏情况时间得到操作序列的最坏情况时间为О(n\^2),但是这不是一个确界。
通过使用聚合分析,考虑整个序列的 n 个操作,可以得到更好的上界。实际上虽然 MULTIPOP 操作的最坏情况时间很高,但是在一个空栈上执行 PUSH、POP、MULTIPOP 的操作序列,代价最多是О(n)。因为我们将一个对象压入到栈后,最多只将其弹出一次,所以一个非空的栈,可以执行的 POP 次数最多为 n。因此上述操作序列最多花费О(n)时间,而一个操作的平均时间为О(n) / n = О(1)。在聚合分析中,我们将每个操作的摊还代价设定为平均代价。所以,这三种操作的摊还代价均为О(1)。
这里我们并未使用概率分析就证明了一个栈操作的平均代价。我们实际上得出的是一个 n 个操作序列的最坏情况运行时间О(n),再除以 n 得到了每个操作的平均代价,或者说摊还代价。
二进制计数器递增
一个 k 位二进制计数器递增的问题的例子。简单来说就是使用二进制来计数,并将这个二进制数放到一个数组中,可以使用一个 INCREMENT 的操作来对这个二进制数增加 1。A.length = k,将最低位保存在 A[0]中,最高位保存在 A[k-1]中。INCREMENT 的伪代码如下:
i = 0
while i < A.length and A[i] == 1
A[i] = 0
i = i+1
if i < A.length
A[i] = 1
如下图所示,在 2~4 行 while 循环时,我们希望将 1 加在第 i 位上。如果 A[i]=1,那么加 1 操作会将第 i 位翻转为 0,并产生一个进位-–—在一次循环中将 1 加到 i+1 位上。否则循环结束,此时若 i
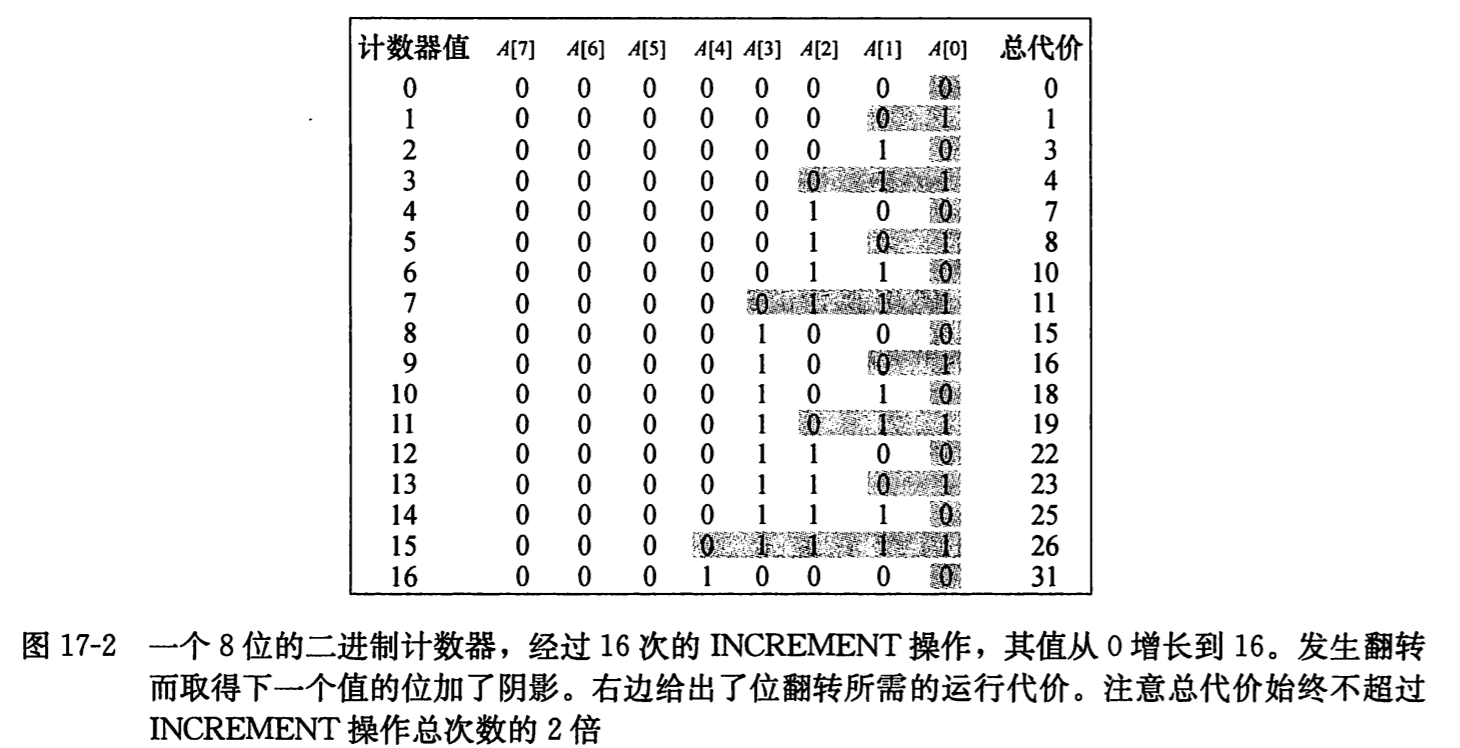
与上一个例子类似,粗略的分析会的到一个正确但是不紧的界。最坏情况下翻转数组上所有的位,INCREMENT 执行一次花费Θ(k)时间,因此 n 个 INCREMENT 的最坏时间为О(nk)。但是通过摊还分析,我们可以得到最坏运行时间О(n),因为不可能每次 INCREMENT 都翻转所有的位。实际上,对一个初值为 0 的计数器,执行 n 个 INCREMENT 的过车给你中,A[i]会翻转 n/(2\^i)次。所以我们可以得到的执行翻转操作的总数为:
 (图片丢失)
(图片丢失)
所以可以得到 n 个 INCREMENT 操作序列的最坏情况时间为О(n),摊还代价为О(n)/n = О(1)。
核算法
用 核算法 进行摊还分析时,我们对不同操作赋予不同费用,赋予某些操作的费用可能多于或少于实际代价。我们将赋予一个操作的费用成为它的*摊还代价*。当一个操作的摊还代价超出其实际代价时,我们将差额存入数据结构中的特定对象,存入的差额成为*信用*。对于后续操作中摊还代价小于实际代价的情况,信用可以用来支付差额。
我们必须小心地选择操作的摊还代价。如果我们希望通过分析摊还代价来证明每个操作的平均代价的最坏情况很小,就应确保操作序列的总摊还代价给出了序列总真实代价的上界。而且,这种关系必须对所有操作序列都成立。数据结构中存储的信用恰好等于总摊还代价与总实际代价的差值。数据结构所关联的信用必须一直非负值,如果在某个步骤,我们允许信用为负值,那么当时的总摊还代价就会低于总实际代价,对于到那个时刻为止的操作序列,总摊还代价就不再是总实际代价的上界了。
栈操作
为了说明摊还分析的核算法,再次使用栈的例子。我们赋予 PUSH、POP、MULTIPOP 如下的摊还代价:
PUSH 2
POP 0
MULTIPOP 0
PUSH 时我们将 1 元的代价支付 PUSH 操作的实际代价,将剩余的 1 元存为信用,这 1 元实际上是作为将来被 POP 时代价的预付费。当执行一个 POP 时,并不缴纳任何费用,而是使用存储的信用来支付其实际代价,对于 MULTIPOP 也是一样的。因为栈中元素的数量总是非负的,所以可以保证信用也非负的。因此,对任意 n 个 PUSH、POP、MULTIPOP 组成的序列,总摊还代价О(n)为总实际代价的上界。
二进制计数器递增
在这个例子中,对一次置位操作,我们设其摊还代价为 2 元,用 1 元支付实际代价,1元存为信用,用来支付将来复位操作的代价。在任何时刻,计数器中任何为 1 的位都存有 1 元信用,这样在复位的时候,我们就不需要支付任何费用了。
INCREMENT 过程一次最多置位一次,因此摊还代价最多为 2 美元,计数器中 1 的个数永远不会为负,所以对于 n 个 INCREMENT 操作的总摊还代价О(n)是总实际代价的上界。
势能法
势能法 摊还分析并不预付代价表示为数据结构中特定对象的信用,而是表示为“势能”,将势能释放即可用来支付未来操作的代价。我们将势能于整个数据结构而不是特定对象相关联。
工作方式如下。对一个初始数据结构 D0 执行 n 个操作,对每个 i=1,2,…,n,令 ci 为第 i 个操作的实际代价,令 Di 为数据结构 Di-1 执行第 i 个操作得到的结果数据结构。*势函数*Φ将每个数据结构 Di 映射到一个实数Φ(Di),此值即为关联到数据结构 Di 的\_势\_。第 i 个操作的 摊还代价 \^ci 用势函数Φ定义为:
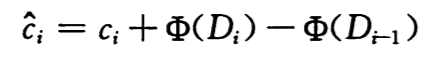
所以每个操作的摊还代价等于其实际代价加上此操作引起的势能变化。则 n 个操作的总摊还代价为
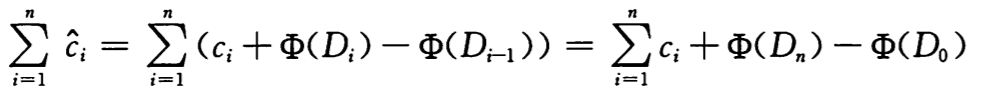
不同的势函数会产生不同的摊还代价,但摊还代价仍未实际代价的上界。在选择势函数时,我们常常发现可以做出一定的权衡,是否使用最佳势函数依赖于对时间界的要求。
两个例子还是盏和二进制计数器,不过势能法分析起来使用公式计算较多,在这里公式写起来不太方便就不详细叙述了。总体思想就是将预支付的代价添加的整个数据结构的势能中,将势能释放即可支付未来操作的代价。
势能法具体的例子可以看下一篇摊还分析动态表的文章,虽然表面上看起来扩张与收缩会有О(n)的代价,但是实际上在表满时将表扩张一倍、装载因子为 1/4 时将表收缩一半的摊还代价仅为О(1)。