贪心算法:赫夫曼编码
赫夫曼编码可以有效地压缩数据,通常可以节省 20%~90%的空间,具体压缩率依赖于数据的特性。我们将待压缩的数据看做字符序列。根据每个字符的出现频率,赫夫曼贪心算法构造出字符的最优二进制表示
假设有一个 10 万个字符的数据文件,它只有 6 个不同的字符,下图给出来了文件中所出现的字符和它们的出现频率。
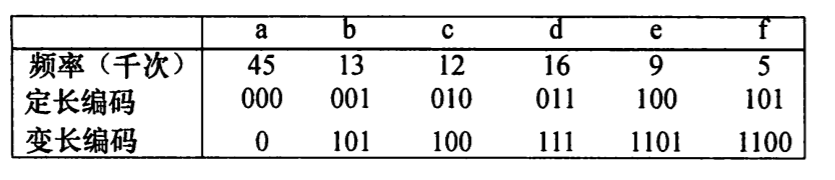
有很多方法可以表示这个文件的信息,在本文中,我们考虑用一种*二进制字符编码*的方法,每个字符用一个唯一的二进制串表示,称为 码字 。如果使用 定长编码 (Fixed-length codeword),需要用 3 位来表示 6 个字符,具体如下图所示。这种方法需要使用 300000 个二进制位才能编码文件。
而 变长编码 (variable-length code)可以达到更好的压缩率,其思想是赋予高频字符短码字,赋予低频字符长码字。具体如上图所示。这种编码方法需要
(45/1 + 13/3 + 12/3 + 16/3 + 9/4 + 5/4) * 1000 = 224 000 位
与定长编码相比,节省了 25%的空间,而且实际上这也是此文件最优的编码方法。
前缀码
前缀码 ,即没有任何码字是其他码字的前缀。且前缀码确实可以保证达到最优数据压缩率。
二进制字符码的编码过程都简单,只要将表示每个字符的码字连接起来即可。前缀码的作用是简化解码过程,由于没有任何码字是其他码字的前缀 i,编码文件的开始码字是无意义的。我们简单的就能识别开始码字并转换回原字符。
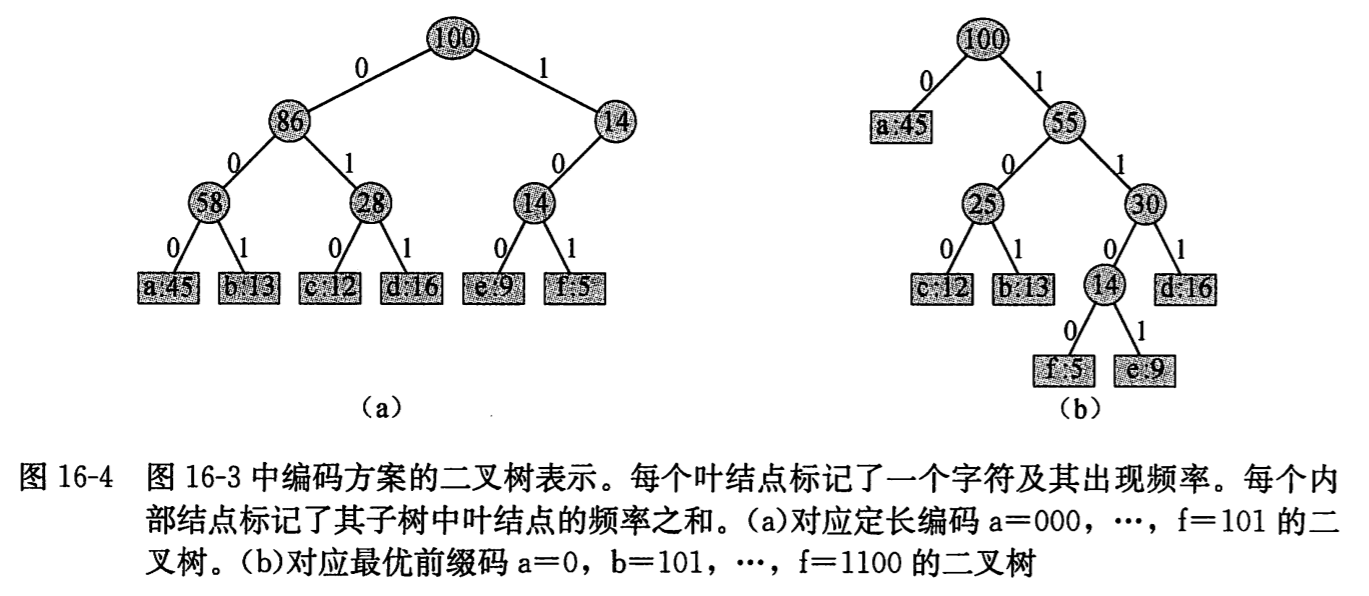
解码过程需要前缀码的一种方便的表示形式,以便我们可以容易地截取开始码字。二叉树可以满足这种需求,其叶结点为给定的字符。一个字符的二进制码字用从根节点到叶结点的简单路径表示,其中 0 意味着转向左孩子,1意味着转向右孩子。如下图所示,a对应定长编码,b对应变长编码。文件的最优编码方案总是会对应一棵满二叉树。
构造赫夫曼编码
赫夫曼设计了一个贪心算法来构造最优前缀码,被成为 赫夫曼编码 。
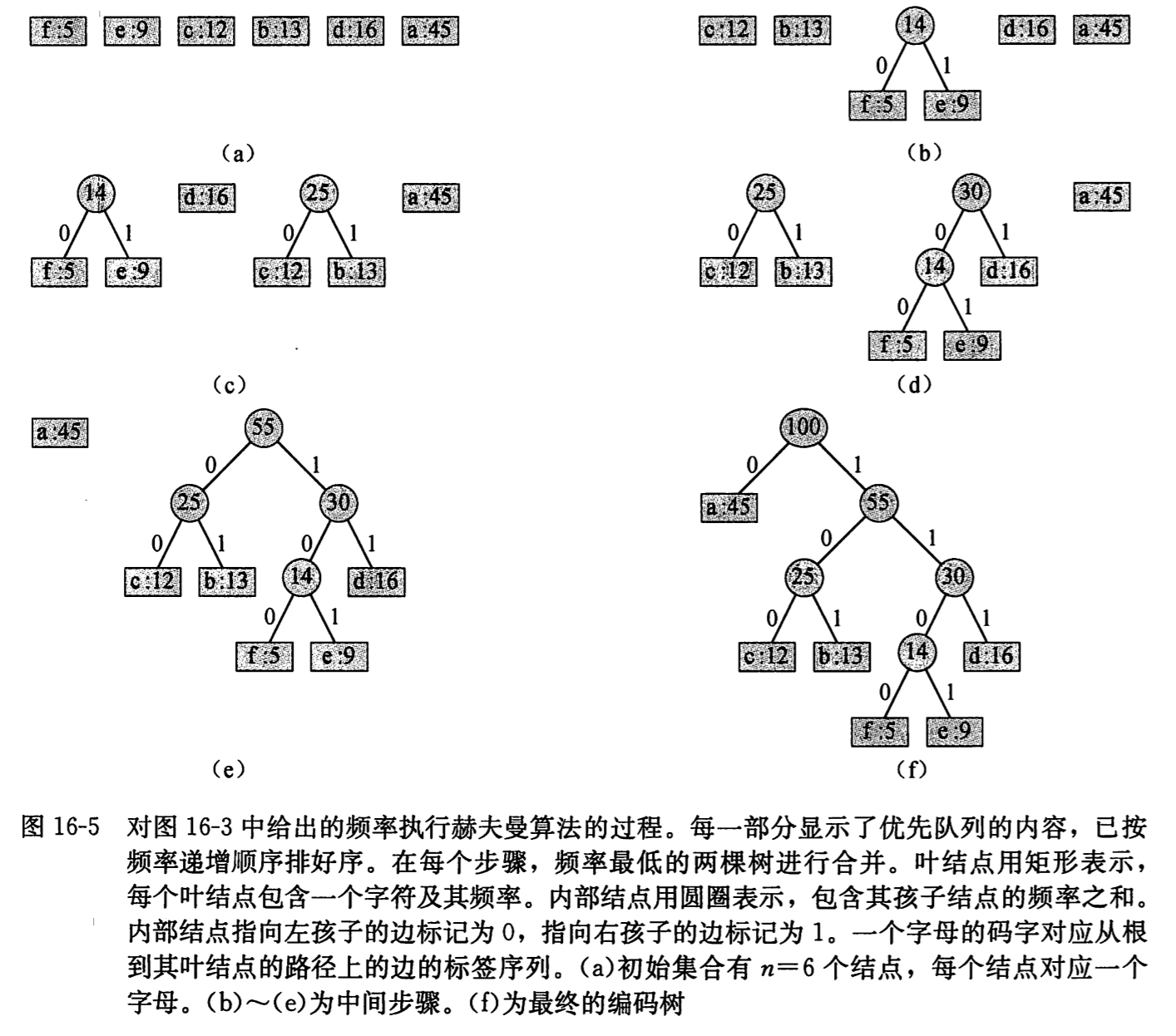
在下面的伪代码中,假定 C 是一个 n 个字符的集合,而其中每个字符 c ∈ C 都是一个对象,其属性 c.freq 表示字符出现的频率,算法自底向上构造出对应最优编码的二叉树。算法使用一个以 freq 为关键字的优先队列Q,以识别两个最低频率的对象将其合并,从|C|个叶结点开始,执行|C|-1 个合并构造出最终的二叉树。
n = |C|
Q = C
for i = 1 to n - 1
allocate a new node z
z.left = x = EXTRACT-MIN(Q)
z.right = y = EXTRACT-MIN(Q)
z.freq = x.freq + y.freq
INSERT(Q, z)
return EXTRACT-MIN(Q) //返回树的根结点
第二行用 C 中的字符初始化优先队列 C,具体执行过程如下图所示:
 (图片丢失)
(图片丢失)
 (图片丢失)
(图片丢失)